1. Kas raksturo kustību?

Bērni šūpojas šūpolēs, snovbordists brauc no kalna un lidmašīna ieskrienas, lai paceltos gaisā. Visās šajās situācijās ir novērojamas kustības, kurām ir noteikts virziens jeb trajektorija un ātrums.

 

  

Atgādinājumu par ķermeņa kustības trajektorijas veidiem var apskatīt šeit.

 

Ikdienā bieži raksturojam kustības ātrumu salīdzinot, kas ir ātrāks vai lēnāks. Piemēram, svīre lidojumā sasniedz lielu ātrumu, bet gliemezis ir daudz lēnāks.

 

 

 

Ir situācijas, kurās mums nepieciešams aprēķināt ātrumu vai noteikt tā skaitlisko vērtību. Automašīnas ārpus apdzīvotas vietas drīkst braukt ar ātrumu \(90\) \(km/h\), bet laika ziņās var uzzināt, ka vēja ātrums ir, piemēram, \(5\) \(m/s\).

 

 

Raksturojot ātrumu, ir svarīgi saprast ar to saistītos jēdzienus. Attālums, kuru veic kāds ķermenis, ir ceļš. Ceļu izsaka garuma mērvienībās - kilometros (\(km\)), metros (\(m\)) vai centimetros (\(cm\)).

Kustības ilgumu noteiktā ceļa garumā raksturo laiks. Laiku izsaka mērvienībās -  stundās (\(h\)), minūtēs (\(min\)) un sekundēs (\(s\)).

 

 

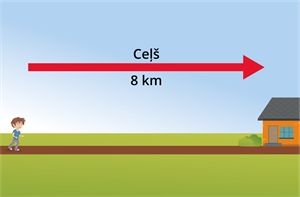
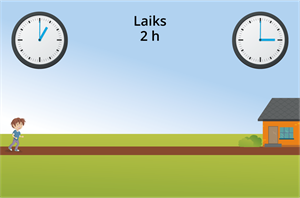
Zinot veikto ceļu un laiku, var aprēķināt ātrumu. Veiktais ceļš ir jādala ar laiku.

Apskatot attēlus, var redzēt, ka zēns iet uz mājām \(8\) \(km\) tālu ceļu, bet laiks kādā šis ceļš tiek veikts, ir \(2\) stundas. Lai noteiktu zēna iešanas ātrumu, noietais ceļš ir jādala ar ceļā veikto laiku. Tātad, \(8 : 2 = 4\). Zēna iešanas ātrums ir \(4\) \(km/h\).

 

Iegaumē, ātruma aprēķināšanas formulu! Vērtīgi izprast, ka, zinot laiku un ātrumu, var aprēķināt arī ceļu, bet, ja no šiem lielumiem nav zināms laiks, arī to var uzzināt.

 

 

 

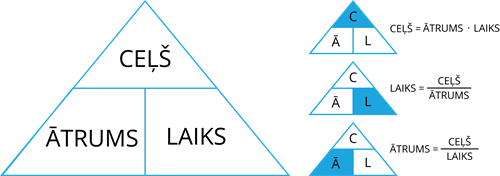
Lai ātrumu varētu korekti aprēķināt un salīdzināt, ir jāizmanto vienādas mērvienības. Ja tās nesakrīt, tad svarīgi mērvienības pārveidot prasītajos lielumos. Starptautiskajā mērvienību sistēmā ceļu mēra metros, bet laiku sekundēs, līdz ar to ātruma mērvienība ir metrs sekundē (\(m/s\)). Kā iepriekš tika minēts, tiek lietoti arī kilometri stundā (\(km/h\)).

 

Lai pārveidotu doto ātrumu mazākās mērvienībās, vari domāt par to, kas notiek laika griezumā (varbūt te kādu veiksmīgāku apzīmējumu). Piemēram, ja zini, ka ķermenis \(36\) \(km\) veic vienas stundas laikā, tad vari aprēķināt, cik lielu ceļa gabalu tas būs veicis \(1\) minūtes laikā, dalot to ar \(60\), jo \(1\) \(h\) \(= 60\) \(min\).
\(36\) \(km\) \(: 60 = 3600\) \(m\) \(: 60 = 600\) \(m\)

Tātad var teikt, ka \(36\) \(km/h\) \(= 600\) \(m/min\). Tu vari domāt par vēl mazāku laika vienību, proti, \(1\) sekundi. Tā kā \(1\) \(min\) \(= 60\) \(s\), tad minūtē veikto ceļu vari samazināt vēl \(60\) reizes.
\(600\) \(m\) \(: 60 = 100\) \(m\).

Seko, ka \(36\) \(km/h\) \(= 600\) \(m/min\) \(= 100\) \(m/s\).

 

Lai labāk izprastu par kustības ātrumu un tā mērvienībām, skaties video šeit.

 

Lai labāk saprastu sakarības starp lielumiem - ceļš, laiks, ātrums, skaties video šeit.

 

Vēlreiz gūt priekšstatu par ātruma aprēķināšanu un situācijām, kuros raksturoti trīs lielumi, var apskatot video šeit.