Brīvās krišanas paātrinājums raksturo cik daudz paātrināsies ķermeņa ātrums, ja ķermenis brīvi krīt.
Par brīvo krišanu sauc ķermeņu vienmērīgi paātrinātu kustību bezgaisa telpā, kad uz ķermeni darbojas tikai smaguma spēks.
Fizikā mūs māca, ka brīvās krišanas paātrinājums uz Zemes ir vienāds ar \(9,8\) un kādēļ šī vērtība ir tieši tāda — apskatīsim šajā tēmā.
Brīvās krišanas paātrinājumu vienkāršotā veidā var aprēķināt no formulas:
, kuru izsaka no formulas , kur
\(F\) ir smaguma spēks vai ķermeņa svars miera stāvoklī vai vienmērīgā taisnvirziena kustībā,
\(m\) ir masa ķermenim, kuru pievelk planēta,
\(g\) ir brīvās krišanas paātrinājums.
Smaguma spēks, kas darbojas uz ķermeni, ir atkarīgs no ķermeņa masas, planētas masas un ķermeņa atrašanās attāluma no planētas centra:
, kur
\(F\) - smaguma spēks, \(N\);
\(G\)- gravitācijas konstante,
;
\(R\) - attālums starp planētas centru un objektu,
\(m\) (ja pievilktais ķermenis atrodas uz planētas virsmas, tad \(R\) ir vienāds ar planētas rādiusu);
\(m\) - planētas un pievilktā ķermeņa masas, \(kg\);
Svarīgi!
Ja savienot abas formulas, tad iegūst formulu , ar kuru var aprēķināt brīvās krišanas paātrinājumu uz jebkura kosmiskā objekta — planētas vai zvaigznes.
Piemērs:
Brīvās krišanas paātrinājumu uz Zemes virsmas aprēķina šādi:
, kur
\(g\) - ir brīvās krišanas paātrinājums;
\(G\) - gravitācijas konstante, ;
- Zemes masa, \(kg\);
- Zemes rādiuss, \(m\).
Mainoties ķermeņa augstumam virs Zemes, mainās brīvās krišanas paātrinājums, jo smaguma spēks, kas darbojas uz ķermeni, samazinās. Brīvās krišanas paātrinājumu noteiktā augstumā \(h\) aprēķina šādi:
Brīvās krišanas paātrinājums uz planētas vai zvaigznes ir atkarīgs no debess ķermeņa masas un debess ķermeņa rādiusa kvadrātā. Tātad, jo lielāka ir zvaigznes masa un jo mazāki ir tās izmēri, jo lielāks ir brīvās krišanas paātrinājums uz tās virsmas.
Balstoties uz brīvās krišanas paātrinājuma aprēķināšanas formulu un iegūtajiem mērījumiem no attāluma, fizikas zinātnieki spēj noteikt brīvās krišanas paātrinājumu uz jebkuras planētas vai zvaigznes, pat ja uz tās reāli nekad nav būts.

Saules sistēmas planētas
Brīvās krišanas paātrinājums uz citi raksturlielumi Saules sistēmas planētām un pundurplanētām:
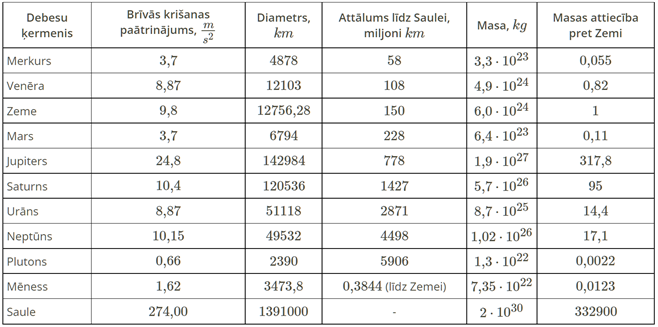
Piemērs:
Neitronu zvaigznēm ir ļoti mazs diametrs, kas var būt mērāms tikai desmitos kilometru, bet to masa ir salīdzināma ar Saules masu, tādēļ to gravitācijas lauks ir ļoti spēcīgs. Ja neitronu zvaigznes diametrs ir \(20\) \(km\) un tās masa ir \(1,4\) reizes lielāka par Saules masu, tad brīvās krišanas paātrinājums ir \(200000000000\) reizes lielāks nekā uz Zemes. Tā vērtība ir apmēram \(2\) . Neitronu zvaigžņu brīvās krišanas paātrinājuma vērtība var sasniegt līdz pat \(7\) .