Skaitļa normālforma.
Skaitļa normālformu fizikā izmanto, lai vienkāršāk pierakstītu ļoti lielus skaitļus (gaismas ātrums, attālumi līdz zvaigznēm u. c.) vai arī ļoti mazus (elektrona masa, gaismas viļņa garums un tml.).
Skaitli normālformā attēlo kā skaitli ar vienu zīmīgo ciparu pirms komata (tātad tas ir skaitlis, kurš lielāks vai vienāds \(1\) un mazāks par \(10\)), kuru reizina ar skaitļa \(10\) pakāpi.
Piemērs:
Ar nelielu kļūdu var apgalvot, ka Mēness attālums no Zemes ir:
\(384000\ \mathrm{km}\) jeb \(\mathrm{km}\).
Ūdeņraža molekulas diametrs ir:
\(0,000000023\ \mathrm{m}\) jeb \(\mathrm{m}\).
Skaitļu pārveidošana normālformā:
a) Veseli skaitļi (komats atrodas skaitļa beigās, ko neraksta):
Atdalām pirmo zīmīgo ciparu ar komatu un saskaitām, par cik ciparu vietām (šķirām) komatu esam pārcēluši uz kreiso pusi - tāda arī būs reizinātāja \(10\) pozitīvā pakāpe.
b) Ļoti mazi skaitļi:
Atdalām pirmo zīmīgo ciparu ar komatu un saskaitām, par cik ciparu vietām (šķirām) komatu esam pārcēluši uz labo pusi - tāda arī būs reizinātāja \(10\) negatīvā pakāpe.
c) Skaitlis ir ar \(10\) pakāpi, bet nav normālformā.
Skaitli bez pakāpes pārveidojam normālformā un izpildām pakāpju saskaitīšanu.
Skaitļu normālformā saskaitīšana un atņemšana - saskaitīt un atņemt var skaitļus ar vienādām pakāpēm:
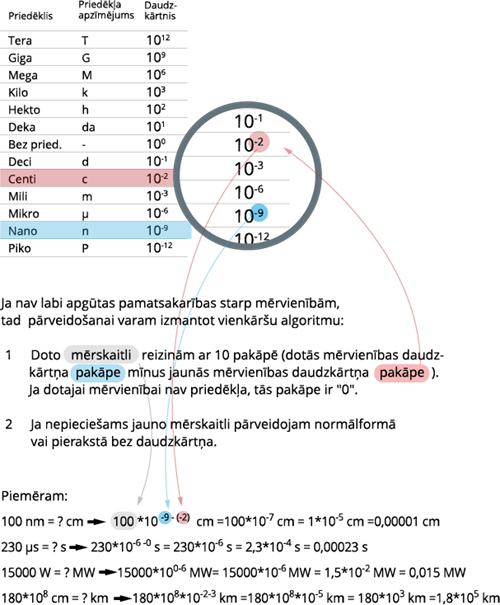
Mērvienību pārveidošana:
Lai veiktu mērvienību pārveidojumus, drīkst (arī eksāmenā) izmantot priedēkļu-daudzkārtņu tabulu un ieteicams iemācīties vienkāršu pārveidošanas algoritmu.