4. Vadoša plakne

Praksē izmanto no vadoša materiāla izgatavotas plaknes, kurām piešķirts elektriskais lādiņš. Lai kvantitatīvi raksturotu šīs plaknes, pieņemam, ka tās ir bezgalīgi lielas. Šādas plaknes tiek raksturotas ne tikai ar piešķirtā lādiņa \(q\) lielumu, bet arī ar virsmas lādiņa blīvumu $\mathrm{\sigma }$, ko var aprēķināt pēc sakarības:

 

$\mathrm{\sigma }=\frac{q}{S}$, kur

 

\(q\) - lādiņš, kas atrodas uz plaknes laukuma \(S\).

 

Teorētiski pierādīts un eksperimentāli noskaidrots, ka šādas plaknes elektriskā lauka intensitāte tās tuvumā visos punktos ir vienāda un nav atkarīga no attāluma.

Uzlādētas, bezgalīgas plaknes elektriskā lauka intensitātes \(E\) moduli aprēķina pēc formulas:

 

$E=\frac{\mathrm{\sigma }}{2{\mathrm{ϵ}}_0}$, kur

$\mathrm{\sigma }$ - elektriskā lādiņa virsmas blīvums, $\frac{\mathrm{C}}{{\mathrm{m}}^2}$,

${\mathrm{ϵ}}_0$ - vakuuma elektriskā konstante ${\mathrm{ϵ}}_0\approx \mathrm{8,9}\cdot {10}^{-12}\frac{\mathrm{F}}{\mathrm{m}}$.

 

Pozitīvi uzlādētas plaknes elektriskā lauka grafiskais attēlojums - intensitātes līnijas "iziet" no pozitīvi lādētas plaknes:

 

 

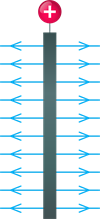
Negatīvi uzlādētas plaknes elektriskā lauka grafiskais attēlojums - intensitātes līnijas "ienāk" negatīvi lādētajā plaknē:

 

 

Praksē plaši tiek izmantota iekārta, kuru veido pozitīvi un negatīvi uzlādētas plaknes. Šādas sistēmas elektriskā lauka attēlojums ir:

 

 

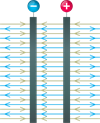
Attēlā redzams, ka ārpus plaknēm intensitāšu līnijas, ko rada katra plakne, vērstas pretējos virzienos - tātad rezultējošais lauks ārpus plaknēm ir "\(0\)".

 

Savukārt, starp plaknēm intensitātes līnijas vērstas vienā virzienā un elektriskā lauka rezultējošā intensitāte ir \(2\) reizes lielāka nekā katras plaknes radītā.