OTRĀ SEMESTRA NOSLĒGUMA TESTI
Ja figūru var pārlocīt uz pusēm tā, ka abas figūras puses sakrīt, tad figūra ir simetriska.
Iegūt simetrisku figūru var lokot, izgriežot vai zīmējot.
Pārliecinoties par simetriju var lokot figūru gan horizontāli, gan vertikāli.
Kvadrāts
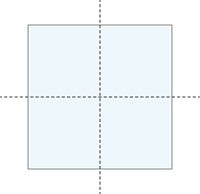
Sešstūris
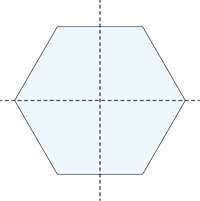
Riņķis
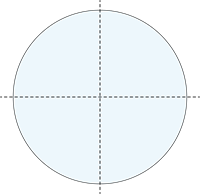
Sirds
Pārliecināties par figūras simetriskumu var vienā vai vairākos veidos. Pārlokot sirds formas figūru horizontāli, abas puses nesakrīt, bet pārlokot to vertikāli, abas puses sakrīt, un mēs varam pārliecināties par šīs figūras simetriskumu.

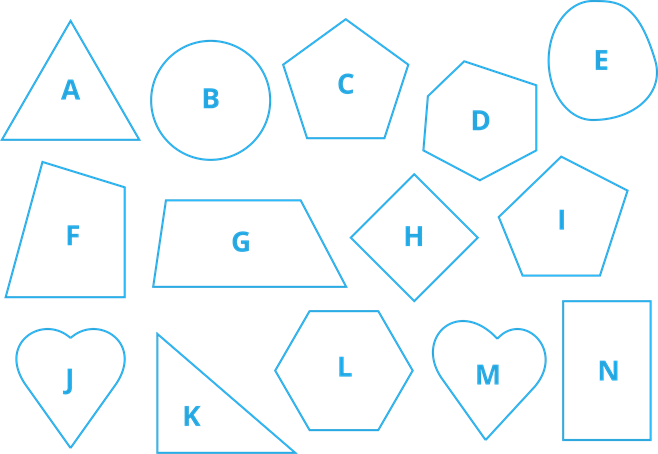
Ne visas ģeometriskas figūras ir simetriskas. No zemāk attēlā dotajām figūrām simetriskas figūras ir: \(A\), \(B\), \(C\), \(H\), \(J\), \(L\) un \(N\). Izpēti un padomā, kāpēc pārējās nav simetriskas?
Simetrisku figūru var uzzīmēt, izmantojot rūtiņu papīru.
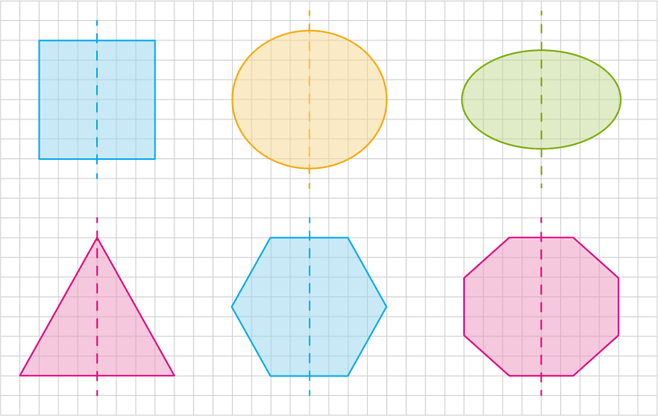
Mums visapkārt var saskatīt dažādas simetriskas lietas un objektus, kuriem abas puses ir ļoti līdzīgas, piemēram, taurenis, lidmašīna, vāze, koku lapas, grāmatu plaukts, māja, dārzs, ceļš. Bet atceries, ka dabā pilnīgi simetriski objekti sastopami ļoti, ļoti reti.

Pamēģini uzzīmēt simetrisku objektu vai figūru arī pats šeit!
