Izteiksme ir uzdevuma skaitlisks pieraksts, kuru aprēķinot var iegūt atbildi uz uzdevumā sniegto jautājumu.
Lai aprēķinātu izteiksmes vērtību, ir jāzina un jāatpazīst darbību locekļi: saskaitāmais, summa, mazināmais, mazinātājs, starpība.

Ja izteiksmē ir saskaitāmie, tos var mainīt vietām, ja nepieciešams, piemēram, lai ērtāk skaitļus būtu saskaitīt.
Piemērs:
\(28\) \(+\) \(15\) \(+\) \(2\)
var samainīt vietām.
\(28\) \(+\) \(2\) \(+\) \(15\)
Tā saskaitīt būs ērtāk.
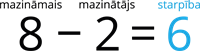
Piemērs:
\(57\) \(-\) \(32\) \(=\) \(25\)
Teksta uzdevumi
Teksta uzdevumus var aprēķināt ar vienu vai vairākām izteiksmēm. Ja risina uzdevumu ar vairākām izteiksmēm, tās pieraksta secīgi, lai soli pa solim atrisinātu teksta uzdevumu.
Teksta uzdevums ar vienu izteiksmi.
Piemērs:

Ievai ir \(15\) grāmatas, Annai \(22\) grāmatas. Cik grāmatu abām meitenēm kopā?
1) \(15\) \(+\) \(22\) \(=\) \(37\) (\(gr.\)) – tik grāmatu abām meitenēm kopā.
Teksta uzdevums ar divām izteiksmēm.
Piemērs:

Ievai ir \(15\) grāmatas, Annai ir par \(7\) grāmatām vairāk. Cik grāmatu abām meitenēm kopā?
1) \(15\) \(+\) \(7\) \(=\) \(22\) (\(gr.\)) – tik grāmatu ir Annai.
2) \(15\) \(+\) \(22\) \(=\) \(37\) (\(gr.\)) – tik grāmatu abām meitenēm kopā.
Jāpievērš uzmanību nosacījumiem:
Cik kopā – tātad būs jāaprēķina summa (\(+\))
Par mazāk – jāatņem (\(-\))
Par vairāk – jāpieskaita (\(+\))
