Ar diviem skaitļiem var veikt dažādas matemātiskās darbības. Tu jau proti izmantot dažādas stratēģijas, aprēķinot summas un starpības \(100\) apjomā:
- skaitlim pieskaitīt viencipara skaitli;
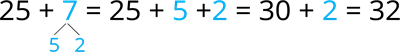
- skaitlim pieskaitīt divcipara skaitli;
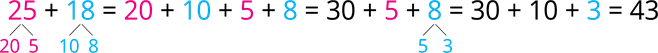
Svarīgi!
Summa nemainās, ja saskaitāmos maina vietām!
Ja esi labi apguvis saskaitīšanas prasmes, tikpat veiksmīgi varēsi aprēķināt arī starpības.
- no skaitļa atņemt viencipara skaitli;
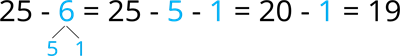
- no skaitļa atņemt divcipara skaitli.
Ja starp trim skaitļiem \(a\), \(b\), \(c\) ir patiesa kaut viena no četrām vienādībām, tad patiesas ir arī pārējās trīs vienādības:
| \(a\) \(+\) \(b\) \(=\) \(c\) |  |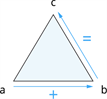
| \(b\) \(+\) \(a\) \(=\) \(c\) |  |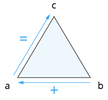
| \(c\) \(-\) \(a\) \(=\) \(b\) |  |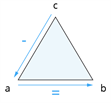
| \(c\) \(-\) \(b\) \(=\) \(a\) |  |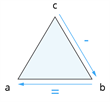
Tādus trīs skaitļus, kam patiesas ir minētās četras vienādības, sauc par draudzīgiem skaitļiem, bet četras vienādības par - draudzīgām vienādībām.
Draudzīgo vienādību piemērs ar saskaitīšanu un atņemšanu.
| \(25 + 18 = 43\) |  |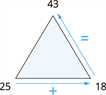
| \(18 + 25 = 43\) |  |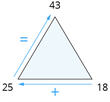
| \(43 - 25 = 18\) |  |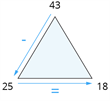
| \(43 - 18 = 25\) |  |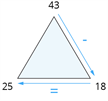
Draudzīgie skaitļi ir \(25\), \(18\), \(43\).
Tu jau esi apguvis reizināšanu un dalīšanu \(100\) apjomā. Reizināšanā, tāpat kā saskaitīšanā, abu skaitļu savstarpējā pārvietošana rezultātu nemaina.
Tāpat kā saskaitīšanā un atņemšanā, arī reizināšanā un dalīšanā ir draudzīgās vienādības.
Ja starp trim skaitļiem \(a\), \(b\), \(c\) ir patiesa kaut viena no četrām vienādībām, tad patiesas ir arī pārējās trīs vienādības:
| \(a\) \(·\) \(b\) \(=\) \(c\) |  |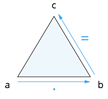
| \(b\) \(·\) \(a\) \(=\) \(c\) |  |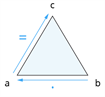
| \(c\) \(:\) \(a\) \(=\) \(b\) |  |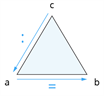
| \(c\) \(:\) \(b\) \(=\) \(a\) |  |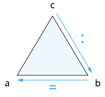
Tādus trīs skaitļus, kam patiesas ir minētās četras vienādības, sauc par draudzīgiem skaitļiem, bet četras vienadības par - draudzīgām vienādībām.
Draudzīgās vienādības piemērs ar reizināšanu un dalīšanu.
| \(7 · 8 = 56\) |  |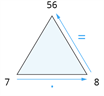
| \(8 · 7 = 56\) |  |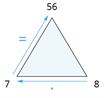
| \(56 : 7 = 8\) |  |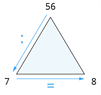
| \(56 : 8 = 7\) |  |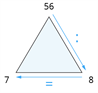
Draudzīgie skaitļi ir \(7\), \(8\), \(56\).
Svarīgi!
Izmanto šīs likumsakarības, lai pārbaudītu iegūto rezultātu un aprēķinātu nezināmo!
Vēlies skaidrojošus video 3. klases matemātikas tēmām?