Četrstūri, kuram visi leņķi taisni, sauc par taisnstūri.
Taisnstūris \(ABCD\)
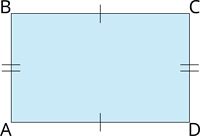
Taisnstūra \(ABCD\) pretējās malas ir \(AB\) un \(CD\).
Malai \(BC\) pretējā mala ir \(AD\).
Taisnstūra pretējo malu garumi ir vienādi.
\(AB = CD\)
\(BC = AD\)
Taisnstūra visu malu garumu summu sauc par perimetru.
Perimetru pieņemts apzīmēt ar burtu \(P\).
Ja taisnstūra \(ABCD\) garums ir \(6\) \(cm\) un platums \(2\) \(cm\), tad perimetru var aprēķināt pēc kārtas saskaitot visu malu garumus

\(P\) \(= 2 + 6 + 2 + 6 = 16\) (\(cm\))
\(P\) \(= 2 · (2 + 6) = 16\) (\(cm\))
\(P\) \(= 2 · (a + b)\)
vai izmantot, ka pretējo malu garumi ir vienādi.
\(P\) \(= 2 + 2 + 6 + 6 = 16\) (\(cm\))
\(P\) \(= 2 · 2 + 2 · 6 = 16\) (\(cm\))
\(P\) \(= 2 · a + 2 · b\)
Taisnstūri, kuram visas malas vienāda garuma, sauc par kvadrātu.
Kvadrāts \(MNOP\).
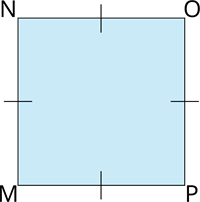
Kvadrāta \(MNOP\) visas malas ir vienāda garuma.
\(MN = NO = OP = PM\)
Ja kvadrāta \(MNOP\) mala ir \(3\) \(cm\) gara, tad tā perimetrs ir \(12\) \(cm\).
\(P\) \(= 3 + 3 + 3 + 3 = 12\) (\(cm\))
\(P\) \(= 3 · 4 = 12\) (\(cm\))