Lai varētu veikli atcerēties un atrast reizinājumus, Tev jāprot izvēlēties sev labāko stratēģiju un paņēmienu. To izvēlēties Tev palīdzēs, ja zināsi reizināšanas īpašības.
Reizināšanas pārvietojamības īpašība
Tāpat kā saskaitāmos, tā arī reizinātājus drīkst mainīt vietām, rezultāts no tā nemainīsies.
Tos maina vietām, lai vieglāk būtu aprēķināt rezultātu.
Reizinātājus drīkst mainīt vietām. Tāpēc abus dotos skaitļus a un b sauc vienādi - par reizinātājiem.
\(a · b = b · a\)
Tāpēc, pierakstot reizināšanas darbību, nav svarīgi, kādā secībā raksta skaitļus, kurus reizina, – rezultāts nemainās.
Piemērs:
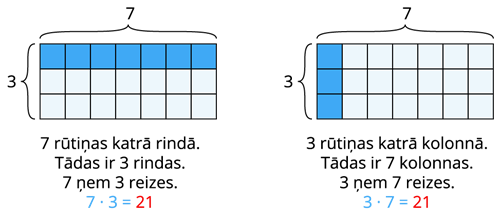
\(7 · 3 = 21\) jeb \(3 · 7 = 21\)
Pārvietot reizinātājus Tu drīksti arī tad, ja izteiksmē ir vairāk nekā viena darbība. Tikai atceries, ka visām darbībām izteiksmē tad jābūt reizināšanas darbībām! Reizinot \(3\) skaitļus, reizinājums nemainās, ja jebkuru divu skaitļu reizinājumu sareizina ar trešo.
Piemērs:
Sareizināsim \(5 · 7 · 2\)!
Izdevīgi sareizināt skaitļus, kuru reizinājums ir pilni desmiti \(5 · 2\), tāpēc reizinātājus pārvietojam tā, lai ir izdevīgāk \(5 · 2 · 7\)!
Izdevīgi sareizināt skaitļus, kuru reizinājums ir pilni desmiti \(5 · 2\), tāpēc reizinātājus pārvietojam tā, lai ir izdevīgāk \(5 · 2 · 7\)!
\(5 · 2 · 7 = 10 · 7 = 70\)