Noskaidrojām, ka taisnstūra laukumu var aprēķināt sareizinot tā malu garumus, jeb garumu un platumu.
Laukumu apzīmē ar burtu \(S\).
Noskaidrojām, ka laukuma mērvienība var būt . Apskatīsim arī citas laukuma mērvienības, un kā tās var iegūt.
Svarīgi!
Atceries, ka \(1\) \(dm\) \(=\) \(10\) \(cm\)!
\(1\) \(dm\) \(·\) \(1\) \(dm\) \(=\) \(1\)
\(10\) \(cm\) \(·\) \(10\) \(cm\) \(=\) \(100\) \(=\) \(1\)

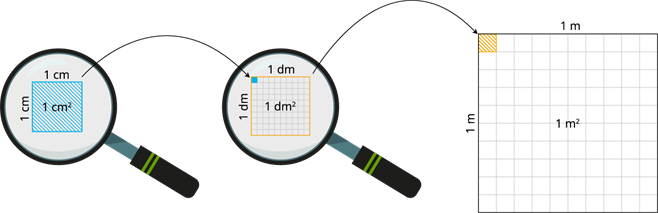
Attēlā ir redzamas divas figūras, kuras pēc laukuma ir vienādas, jo abām figūrām garums un platums ir vienāds \(1\) \(dm\) \(=\) \(10\) \(cm\). Līdz ar to arī figūru laukumi ir vienādi.
Apskati doto attēlu, laukuma mērvienības!
Svarīgi!
\(1\) \(=\) kvadrātcentimetrs.
Tā ir laukuma vienība, ar kuru var noklāt laukumu, kur katra mala ir \(1\) \(cm\).
\(1\) \(=\) kvadrātdecimetrs.
Tā ir laukuma vienība, ar kuru var noklāt laukumu, kur katra mala ir \(1\) \(dm\).
\(1\) \(=\) ir kvadrātmetrs.
Tā ir laukuma vienība, ar kuru var noklāt laukumu, kur katra mala ir \(1\) \(m\).
Attēlā ir redzams, ka \(1\) veidojas no kvadrāta, kuram garums un platums ir \(1\) \(cm\).
Savukārt šāds \(1\) aizņem tikai vienu rūtiņu no visa \(1\) . Jo \(1\) \(dm\) \(=\) \(10\) \(cm\) un \(1\) \(=\) \(100\) .
Kā arī šāds \(1\) aizņem tikai vienu rūtiņu \(1\) , jo \(1\) \(m\) \(=\) \(10\) \(dm\) un \(1\) \(=\) \(100\)
Laukuma vienības var būt arī:
\(1\) - kvadrātmilimetrs
\(1\) - kvadrātkilometrs
\(1\) \(a\) - ārs
\(1\) \(ha\) - hektārs
Iepazīsti laukuma mēru pārveidojumus!
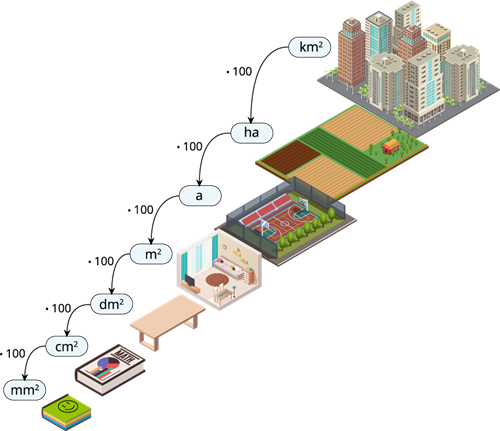
Lai noskaidrotu cik \(1\) ietilpst , \(1\) ir jāreizina ar \(100\), jeb \(1 · 100 = 100\) .
Tātad, \(1\) ietilpst \(100\) .
Šī sakarība darbojas ar visiem laukuma mēriem, pārveidojot no lielākas mēra vienības uz mazāku! Ja vēlies pārveidot no mazākas uz lielāku laukuma mēra vienību, izmanto dalīšanu!
Nākamajos divos attēlos var redzēt, ka \(1\) \(ha\) ir mazāks nekā \(1\) .
\(1\) \(ha\) ir \(100\) reižu mazāks nekā \(1\) .

\(1\) \(ha\) \(=\) \(100\) \(m\) \(· 100\) \(m\) \(= 10000\)
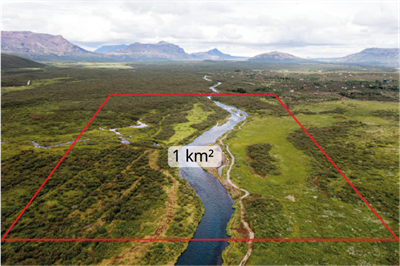
\(1\) \(= 1000\) \(m\) \(· 1000\) \(m\) \(= 1000000\)


