1. Jauktu skaitļu saskaitīšana un atņemšana

Atceries! Jaukts skaitlis ir vesela skaitļa un daļskaitļa summa, kur summas zīmi neraksta.

Ja divu jauktu skaitļu summu būtu četru saskaitāmo summa.

Saskaitīšanas īpašības turklāt saka, ka saskaitāmos summā var mainīt vietām un pārgrupēt. To ievērojot, otro saskaitāmo var mainīt vietām ar trešo un saskaitīt savā starpā pirmo ar otro un trešo ar ceturto.

Savukārt, te var atcerēties, ka vesela skaitļa un daļskaitļa summu var pierakstīt, kā jauktu skaitli, \(+\) zīmi nerakstot.

Var secināt! Lai saskaitītu jauktus skaitļus, veselos skaitļus var saskaitīt savā starpā, bet daļskaitļus var saskaitīt savā starpā.

 

 

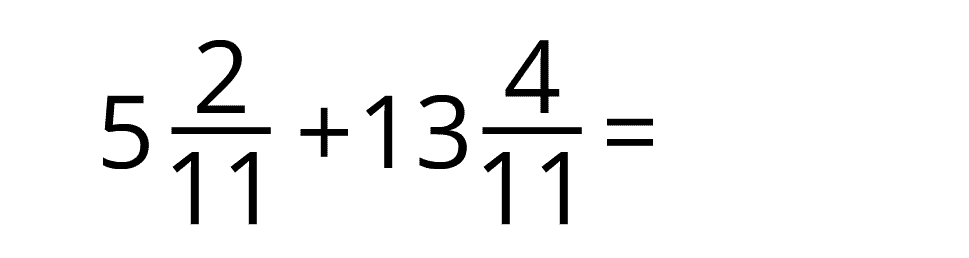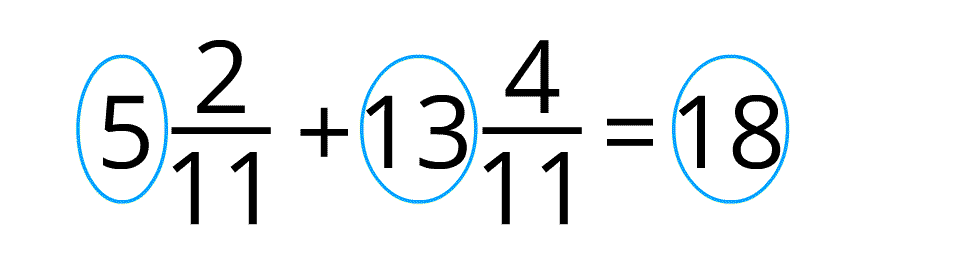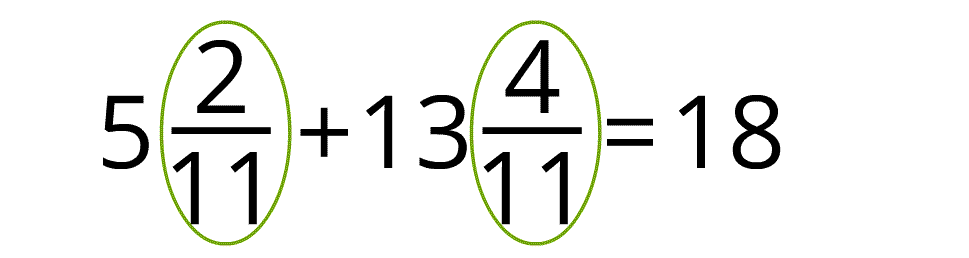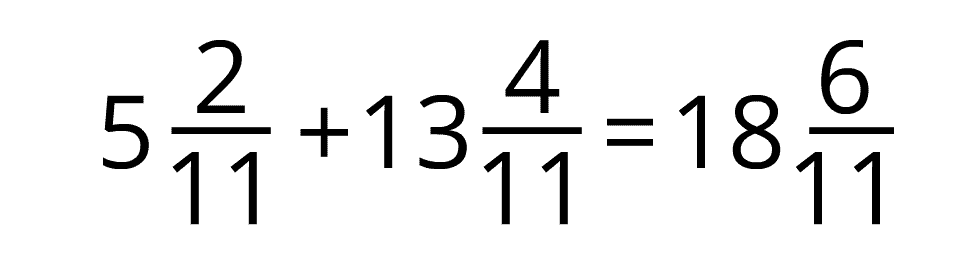
Ja saskaitot daļskaitļus, iegūst neīstu daļu, tad izsaka veselos. Atceries vienmēr pārliecināties, ka, ko norādi, kā atbildi, nav saīsināma. Ja tā tomēr ir saīsināma, tad veido sev ieradumu daļskaitli rezultātā saīsināt!

Padomā! Ko nozīmē atņemt summu?

Tu zini, ka \( 15 - 7 = 8\). Skaitli \(7\) var arī uzrakstīt kā summu \(4+3\). Kā atņemt no \(15\) summu \(4+3\), lai saglabātu to pašu rezultātu \(8\)? Jāatņem katrs saskaitāmais.

\(15 - (4 + 3) = 15 - 4 - 3 = 8\)

Tāpat arī rīkosimies, atņemot jauktu skaitli no jaukta skaitļa, atceroties, ka jaukts skaitlis ir vesela skaitļa un daļskaitļa summa.

Var secināt! Lai atņemtu jauktus skaitļus, veselos skaitļus var atņemt savā starpā, bet daļskaitļus var atņemt savā starpā.

 

 

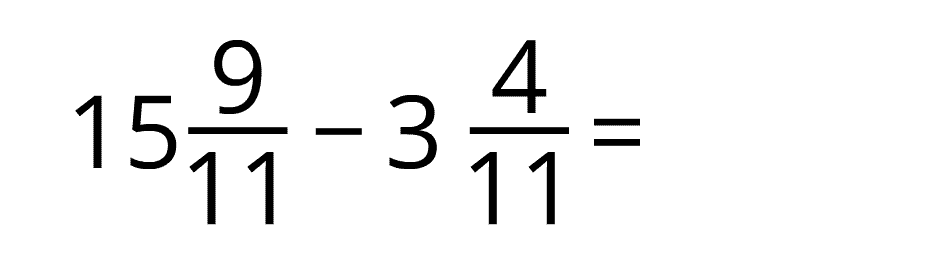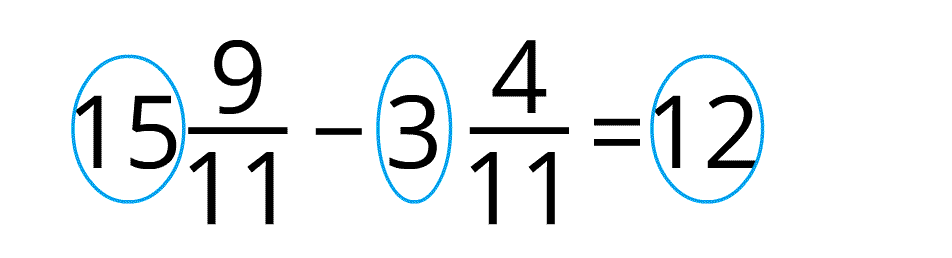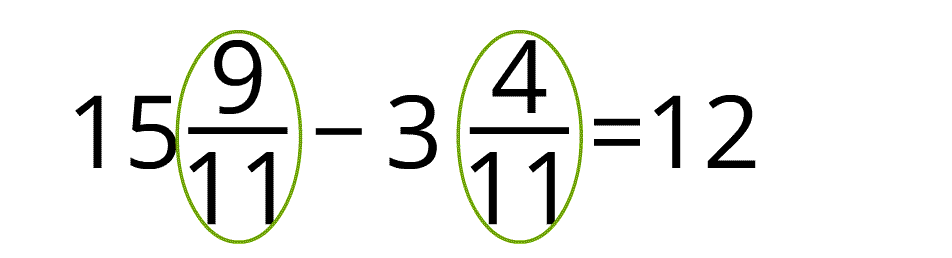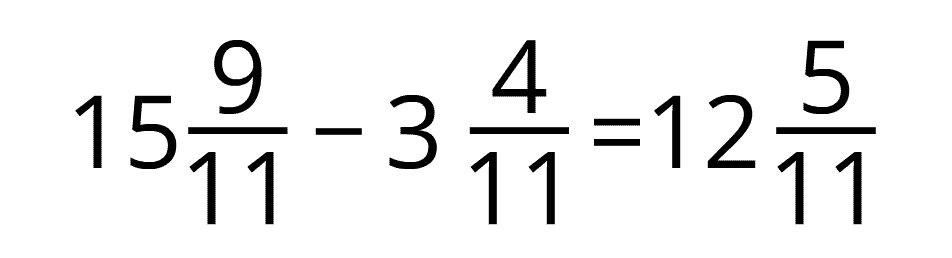
Ja gadās situācija, kad daļskaitļus nevar atņemt, jo mazināmā daļskaitlis ir mazāks nekā mazinātāja daļskaitlis, vienmēr var paplašināt daļu - aizņemties \(1\) veselu no veselajiem un atdot to daļām.