Daļas pamatīpašība. Saīsināšana un paplašināšana — teorija. Matemātika (Skola2030), 5. klase.

Kāda daļa šai taisnstūrī ir iekrāsota? Izpēti zīmējumu!

YCUZD_230721_5374_taisnstūris.svg

1) Taisnstūris ar divām tumšākām līnijām sadalīts \(3\) vienādās daļās.

Redzam, ka

\frac{2}{3}

no taisnstūra ir dzeltenā krāsā.

2) Šis taisnstūris ir sadalīts arī \(18\) rūtiņās.

Saskaitām rūtiņas un redzam, ka

\frac{12}{18}

ir dzeltenas.

Tātad

\frac{2}{3} = \frac{12}{18}

, jo ir viens un tas pats taisnstūra dzeltenais laukums.

Aplūkojam uzmanīgāk iegūto vienādību, otrajai daļai saucējs un skaitītājs ir tieši \(6\) reizes lielāki nekā pirmajai. Pirmajai daļai attiecīgi abi \(6\) reizes mazāki.

YCUZD_220726_4145_daļas_8.svg

Matemātikā ir spēkā likums, kuru sauc par daļas pamatīpašību:

Daļas lielums nemainās, ja tās skaitītāju un saucēju reizina vai dala ar vienu un to pašu skaitli, kas nav \(0\).

Skaitli, ar kuru daļu paplašina, matemātikā sauc par papildreizinātāju.

Paplašināt daļu, piemēram, ar \(3\), nozīmē katru gabalu sadalīt \(3\) mazākos gabalos, bet saīsināt ar \(3\) nozīmē ik pa trīs gabaliem apvienot - izveidot lielākus gabalus.

Saīsināšana un paplašināšana ir pretējas darbības.

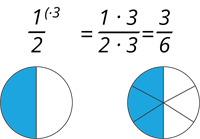
YCUZD_221114_4692_apļi.png

YCUZD_221114_4692_apļi_1.png

Piemērs:

Daļu

\frac{2}{3}

paplašinot ar \(2\), \(4\), \(6\), \(10\) vai \(12\), var iegūt vairākas pēc lieluma vienādas daļas:

\begin{array}{l} {\frac{2}{3}}^{(\cdot 2} = \frac{4}{6} \\ {\frac{2}{3}}^{(\cdot 4} = \frac{8}{12} \\ {\frac{2}{3}}^{(\cdot 6} = \frac{12}{18} \\ {\frac{2}{3}}^{(\cdot 10} = \frac{20}{30} \\ {\frac{2}{3}}^{(\cdot 12} = \frac{24}{36} \\ \frac{2}{3} = \frac{4}{6} = \frac{8}{12} = \frac{12}{18} = \frac{20}{30} = \frac{24}{36} \end{array}

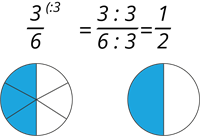
Piemērs:

Daļu

\frac{50}{100}

saīsinot ar \(2\), \(10\), \(25\) vai \(50\), var iegūt vairākas pēc lieluma vienādas daļas:

\begin{array}{l} {\frac{50}{100}}^{(: 2} = \frac{25}{50} \\ {\frac{50}{100}}^{(: 10} = \frac{5}{10} \\ {\frac{50}{100}}^{(: 25} = \frac{2}{4} \\ {\frac{50}{100}}^{(: 50} = \frac{1}{2} \\ \frac{50}{100} = \frac{25}{50} = \frac{5}{10} = \frac{2}{4} = \frac{1}{2} \end{array}

Vienādas daļas taisnstūros

YCUZD_220726_4145_daļas_1.svg

Tātad

\frac{1}{3} = \frac{2}{6} = \frac{4}{12}

YCUZD_220726_4145_daļas_2.svg

Var redzēt, ka

\frac{3}{4} = \frac{6}{8} = \frac{9}{12} = \frac{12}{16}

Daļas atrašanās uz skaitļu stara

Uz skaitļu stara vienam punktam var atbilst dažādi pierakstītas daļas. Piemēram, zīmējumā var redzēt, ka

\frac{5}{10} = \frac{1}{2}

.

YCUZD_220726_4145_daļas_3.svg

Piemērs:

Dotajam skaitļu staram starp \(0\) un \(1\) ir \(8\) iedaļas. Katra iedaļa ir

\frac{1}{8}

no šī garuma.

Burta \(A\) vērtība ir

\frac{2}{8}

, ko varam vēl saīsināt ar \(2\).

\(A\) \(=\)

\frac{1}{4}

.

\(B\) \(=\)

\frac{3}{8}

. Šo daļu nevar saīsināt.

\(C\) \(=\)

\frac{4}{8}

\(=\)

\frac{1}{2}

.

Svarīgi!

Skaitļi

\frac{a}{1}

un

a

nozīmē vienu un to pašu, jeb

\frac{a}{1}

\(=\)

a

.

Piemērs:

\frac{5}{1}

\( = 5\),

\frac{12}{1}

\(= 12\), \(27 =\)

\frac{27}{1}

Iepriekšējā tēma

Atgriezties tēmā

Nākamā teorija

Nosūtīt atsauksmi

Atradi kļūdu?

Sūti mums ziņu!