Ikdienā saskaroties ar daļskaitļiem, bieži vien darbojamies tieši ar daļas vērtību no kaut kāda veseluma. Vienam un tam pašam daļskaitlim var būt dažādas vērtības, atkarībā no tā, kāds dotajā situācijā ir izvēlētais veselums jeb veselais.
Piemērs:
Ja tu zini, ka varēsi apēst viens pats picas, tad tās būs trīs šķēles, kuras tu iegūsi, sagriežot veselu picu četrās vienādās šķēlēs. Vai tu būsi kārtīgi paēdis vai tikai panašķojies, būs atkarīgs no tā, cik liela ir veselā pica. būs dažāda vērtība atkarībā no tā, cik lielu picu tu izvēlēsies.
Aplūkosim dažādas situācijas, kurās atpazīsim daļu, tās vērtību un veselo.
Piemērs:
\(5\). a klasē ir \(15\) meitenes, kas ir no \(25\) klases skolēniem. \(5\). b klasē jeb \(20\) no visiem \(30\) skolēniem ir zēni. \(5\). c klasē, kurā mācās \(28\) skolēni, jeb \(7\) skolēni apmeklē skolas volejbola nodarbības.
Situācija | Veselais | Daļa | Daļas vērtība |
\(5\). a klase | \(25\) skolēni | \(15\) meitenes | |
\(5\). b klase | \(30\) skolēni | \(20\) zēni | |
\(5\). c klase | \(28\) skolēni | \(7\) volejbolisti |
Kā aprēķināt daļas vērtību, ja ir dots veselais?
Pati svarīgākā informācija ir izteikta ar daļskaitli. Atceries! Daļas saucējs norāda, cik vienādās daļās ir sadalīts vai no cik vienādām daļām sastāv veselais. Daļas skaitītājs, savukārt, izsaka, cik tieši no vienādajām daļām ir jāpaņem.
Piemērs:
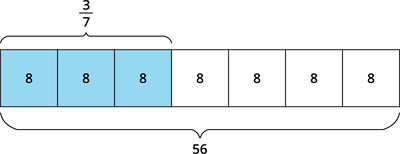
Tā kā veselais ir \(56\), tad daļas saucējs norāda, ka tas ir jāsadala \(7\) vienādās daļās, bet skaitītājs ziņo, ka jāpaņem tieši \(3\) no septiņām daļām.
Kā aprēķināt veselo, ja ir dota daļas vērtība?
Šajā situācijā ir jādomā pretēji tam, kā daļas vērtība tiek iegūta. Kas ir pēdējais solis, aprēķinot daļas vērtību, tas apgrieztā situācijā būtu pirmais. Daļas skaitītājs norāda, cik daļas jāpaņem. Tātad daļas vērtību veido tik daļas, cik ir saucējs, no kurienes var aprēķināt pamatdaļas vērtību. Savukārt, saucējs pastāsta, no cik pamatdaļām veidojās veselais.
Piemērs:
Mārītes penālī no visiem rakstāmrīkiem ir tieši \(12\) krāsu zīmuļi. Cik pavisam rakstāmrīku ir Mārītes penālī?
Varam spriest šādi. \(12\) zīmuļi tika iegūti, kad visi rakstāmrīki tika sadalīti \(5\) vienādās daļās, no kurām tika paņemtas tieši \(3\). Ja \(12\) dalīs ar \(3\), tad varēs noskaidrot, cik rakstāmrīku ir vienā no piecām daļām. Iegūto skaitli sareizinot ar \(5\), var noskaidrot, cik pavisam rakstāmrīku ir penālī.
vērtība
jeb veselā vērtība


