Ja lielāko skaitli dala ar mazāko, tad uzzinām, cik reizes tas ir lielāks par mazāko skaitli.
Toties, ja mazāko skaitli dalām ar lielāko skaitli, tad uzzinām, kāda daļa no lielākā skaitļa ir mazākais skaitlis.
Divu skaitļu dalījuma pieraksts ir šo skaitļu attiecība.
Aplūkosim attēlu!

Nogrieznis \(AB\) ir \(4\) reizes garāks par nogriezni \(CD\), tad abu nogriežņu attiecību var uzrakstīt šādi:
\(AB : CD = 4 : 1\ \)
Bet pieraksts \(CD : AB = 1 : 4\) norāda, ka nogriežņa \(CD\) garums ir ceturtā daļa no nogriežņa \(AB\) garuma.
To lasa: \(CD\) attiecība pret \(AB\) ir \(1\) pret \(4\).
Divu skaitļu attiecību var pierakstīt:
- ar dalīšanas zīmi \((\)\(1:4)\);
- ar daļsvītru ;
- ar vārdu pret \((\)\(1\) pret \(4)\).
Piemērs:

Svarīgi!
Attiecībās var salīdzināt tikai viena un tā paša lieluma skaitliskās vērtības, piemēram, kāda ir \(4\ m\) un \(20\ cm\) attiecība, bet kāda ir \(4\ kg\) un \(20\ cm\) attiecība, nevar.
Piemērs:
Nogriežņa \(KM\) garums ir \(9\) vienības.
- Sadali šo nogriezni divos nogriežņos \(KB\) un \(BM\) tā, lai to attiecība starp daļām būtu \(2 : 7\).
Risinājums:
Viss nogrieznis jāsadala \(9\) vienādās daļās, jo \(2+7=9\).
Pirmajam nogrieznim \(KB\) garums ir \(2\) vienības, bet nogriežņa \(BM\) garums ir \(7\) vienības.
- Sadali šo pašu nogriezni \(KM\) trijās daļās tā, lai šo daļu attiecības būtu \(1:3:5.\)
Risinājums:
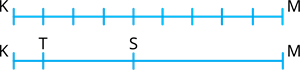
Rīkojas līdzīgi. Vispirms nosaka, cik vienībās jāsadala viss nogrieznis (\(1+3+5=9\)). Pēc tam atrod atbilstošo vienību lielumus \(KT : TS : SM = 1 : 3 : 5\)