Funkciju, kuru apraksta vienādojums , kur un , sauc par kvadrātfunkciju.
- visu reālo skaitļu kopa,
\(x\) - neatkarīgais mainīgais jeb arguments,
\(y\) - atkarīgais mainīgais jeb funkcijas vērtība,
\(a\) - funkcijas kvadrātlocekļa koeficients,
\(b\) - funkcijas lineārā locekļa koeficients,
\(c\) - funkcijas brīvais loceklis (viens pats skaitlis).
Funkcijas definīcijas apgabals (pieļaujamās argumenta \(x\) vērtības) ir visu reālo skaitļu kopa ().
Kvadrātfunkcijas grafiku sauc par parabolu.
Funkcija \(y =x^2\) ir kvadrātfunkcijas speciāls gadījums, kad \(a=1\), \(b=0\), \(c=0\).
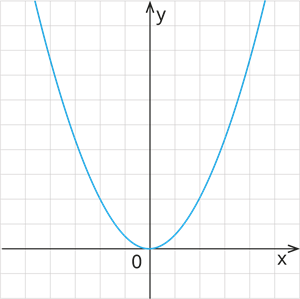
Šo grafiku konstruē, izmantojot vērtību tabulu:
\(x\ \) | \(-3\) | \(-2\ \) | \(-1\) | \(0\) | \(1\) | \(2\) | \(3\) |
\(y\ \) | \(9\) | \(4\ \) | \(1\) | \(0\) | \(1\) | \(4\) | \(9\) |
Ievēro: parabolas virsotne ir \((0; 0)\).
