Nevienādība ar diviem mainīgajiem — teorija. Matemātika (Skola2030), Matemātika I.

Nevienādību, kas satur divus nezināmos lielumus, sauc par nevienādību ar diviem mainīgajiem.

Piemēram:

x - 3 y > 4

x^{2} + y^{2} \leq 4

xy - 6 x \geq 1

Nevienādības, kas satur divus mainīgos $x$ un $y$, atrisinājumu kopa ir visi skaitļu pāri $(x;y)$, ko ievietojot dotajā nevienādībā mainīgo vietā iegūst patiesu skaitlisku nevienādību.

Nevienādības ar diviem mainīgajiem atrisinājumu kopu jeb visus atrisinājumus var attēlot grafiski. Šādu nevienādību atrisinājumu kopas ģeometriskais attēls ir plaknes daļa.

Lai atrisinātu šādas nevienādības, parasti:

izsaka $y$ kā $x$ funkciju (izņemot gadījumu, kad tā ir riņķa līnija vai reizinājums);
nevienādības zīmi aizstāj ar vienādības zīmi;
konstruē šīs funkcijas grafiku;
iesvītro nevienādībā prasīto plaknes daļu;
izdara secinājumus par grafika piederību atrisinājumam.

Piemērs:

Nosaki nevienādības

2 x + y > - 2

atrisinājumu kopu.

Risinājums.

Izsaka

y > - 2 x - 2

Redzam, ka dota lineāra funkcija

y = - 2 x - 2

, kuras grafiks ir taisne. Sastāda vērtību tabulu, iegūst grafiku.

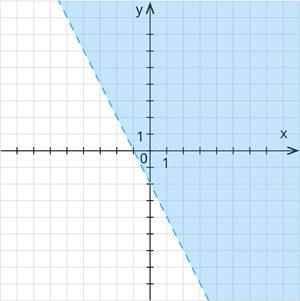
Iekrāso to plaknes daļu, kura atrodas virs taisnes, jo ir spēkā nevienādība

y > f (x)

Stingrām nevienādībām (<; >) grafiku attēlo ar pārtrauktu līniju, jo funkcijas grafikam piederošie punkti nepieder nevienādības atrisinājumam.

Atbilde: Atrisinājumu veido iekrāsoto punktu kopa, taisnes

y = - 2 x - 2

punkti nepieder atrisinājumam.

Piemērs:

Nosaki nevienādības

x^{2} + 4 x \leq y - 2

atrisinājumu kopu.

Risinājums.

Izsaka

y

\begin{array}{l} - y \leq - x^{2} - 4 x - 2 | : (- 1) \\ y \geq x^{2} + 4 x + 2 \end{array}

Uzrakstot kā vienādību, var redzēt, ka ir dota kvadrātfunkcija

y = x^{2} + 4 x + 2

Konstruē parabolu un iekrāso visu to punktu koordinātas, kuras atrodas virs parabolas (skat zīm.). Punkti, kas atrodas uz parabolas pieder atrisinājumu kopai (jo nestingrā nevienādības zīme

\geq

Lai pārliecinātos, ka iekrāsota pareizā plaknes daļa, tad no iekrāsotā apgabala izvēlas vienu punktu un pārbauda, vai tā koordinātas der par dotās nevienādības atrisinājumu.

Piemēram, $(-1;2)$