Vienādojuma cos x=a atrisināšana no vienības riņķa — teorija. Matemātika (Skola2030), Matemātika I.

Vienādojumu $cosx=a$ ērti atrisināt, izmantojot vienības riņķa līniju. Trigonometriskais vienības riņķis ir dots matemātikas eksāmena formulu lapā.

Atrisināsim vienādojumu

cosx = \frac{\sqrt{2}}{2}

Uz kosinuss ass atliksim vērtību

\frac{\sqrt{2}}{2}

. Ir divi pagrieziena leņķi, kuru kosinuss ir

\frac{\sqrt{2}}{2}

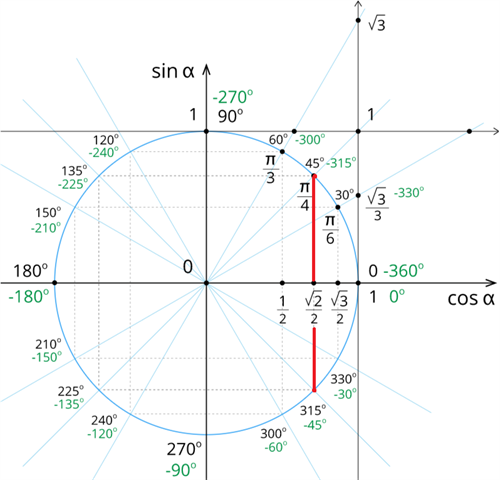
Tie ir leņķi

\frac{π}{4} jeb 45 °

- \frac{π}{4} jeb - 45 °

Tā kā pieskaitot vai atņemot vienu vai vairākas reizes pilnu leņķi

2 π

, atkal iegūst pagrieziena leņķi, kura kosinuss ir

\frac{\sqrt{2}}{2}

, tad vienādojumam ir bezgalīgi daudz atrisinājumu.

Vienādojuma

cosx = \frac{\sqrt{2}}{2}

atrisinājums ir

\begin{array}{l} x = [\begin{array}{l} \frac{π}{4} + 2 π n \\ - \frac{π}{4} + 2 π n \end{array} \\ n \in ℤ \end{array}

Ja izsaka ar grādiem, nevis radiāniem, tad

\begin{array}{l} x = [\begin{array}{l} 45 ° + 360 ° n \\ - 45 ° + 360 ° n \end{array} \\ n \in ℤ \end{array}

Šīs atbildes var apvienot vienā:

x = \pm \frac{π}{4} + 2 π n, n \in ℤ

jeb

x = \pm 45 ° + 360 n, n \in ℤ

Piemērs:

\cos x = - \frac{1}{2}

x = \pm \frac{2 π}{3} + 2 π n, n \in ℤ

, ja atbildi pieraksta ar radiāniem

x = \pm 120 ° + 360 ° n, n \in ℤ

, ja atbildi pieraksta ar grādiem.

Iegaumē atrisinājums šādiem vienādojumiem (visur atrisinājumos $n\in\mathbb{Z}$):

Atceries!

Vienādojumam $\cos x = a$ eksistē atrisinājums, ja $-1\leq a\leq 1$ jeb $|a|\leq 1$.

Vienības riņķis formulu lapā

Atradi kļūdu?

3. Vienādojuma cos x=a atrisināšana no vienības riņķa