Vienpusējas robežas definīcija — teorija. Matemātika (Skola2030), Matemātika II.

Video mācību materiāli

"MATEMĀTIKA II"

Definējot robežu

\lim_{x \to a} f (x)

, pieņem, ka argumenta \(x\) vērtība var būt jebkurš skaitlis no punkta \(a\) apkārtnes: gan tāds, kas lielāks nekā skaitlis \(a\), gan arī tāds, kas ir mazāks nekā \(a\) (izņemot pašu skaitli \(a\)). Taču praksē pēta funkcijas izturēšanos gadījumos, ja arguments tiecas uz \(a\) tikai no vienas puses: no labās puses (tad \(x>a\)) vai no kreisās puses (tad \(x<a\)).

Funkcijas robežu, kad

x \to a

x > a

, sauc par robežu no labās puses vai par labo robežu un raksta

\lim_{x \to a + 0} f (x)

Funkcijas robežu, kad

x \to a

x < a

, sauc par robežu no kreisās puses vai par kreiso robežu un raksta

\lim_{x \to a - 0} f (x)

Piemērs:

Funkcija

f (x) = \frac{4}{x}

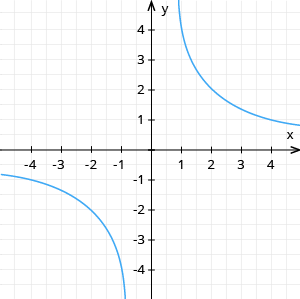
Abpusējās robežas var nolasīt no grafika. Taču tās var iegūt arī, izdarot loģiskus spriedumus.

\lim_{x \to 0 - 0} \frac{4}{x} = - \infty

. Spriedumi: pozitīvu skaitli 4 dalot ar pēc patikas mazu negatīvu skaitli, iegūst pēc patikas lielu negatīvu skaitli.

\lim_{x \to 0 + 0} \frac{4}{x} = + \infty

. Spriedumi: pozitīvu skaitli 4 dalot ar pēc patikas mazu pozitīvu skaitli, iegūst pēc patikas lielu pozitīvu skaitli.

Uzdevums.

Nosaki

\lim_{x \to 0 - 0} \frac{- 1}{x}

\lim_{x \to 0 + 0} \frac{- 1}{x}

Risinājums.

\lim_{x \to 0 - 0} \frac{- 1}{x} = \frac{- 1}{- 0} = + \infty

\lim_{x \to 0 + 0} \frac{- 1}{x} = \frac{- 1}{+ 0} = - \infty

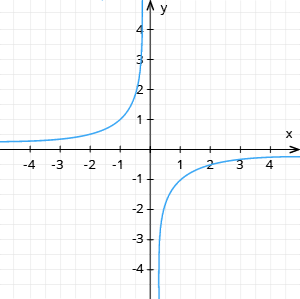
Lietderīgi ir aprēķināt arī robežas, kad \(x\) tiecas uz bezgalību. Arī šajā gadījumā apskata divas robežas, bet tās nav vienpusējās robežas.

\lim_{x \to + \infty} \frac{- 1}{x} = \frac{- 1}{+ \infty} = - 0

, tātad grafiks tuvojas nullei (x asij) no apakšas.

\lim_{x \to - \infty} \frac{- 1}{x} = \frac{- 1}{- \infty} = + 0

, tātad grafiks tuvojas nullei (x asij) no augšas.

Skat. funkcijas

f (x) = \frac{- 1}{x}

grafiku

Rekomendācija. Labi uzdevumi par vienpusējām robežām atrodami grāmatā Dainis Kriķis. Kārlis Šteiners. Matemātiskās analīzes elementi vidusskolai 1. daļa. Zvaigzne ABC. 59. lpp.

Atsauce:

Materiālu sagatavoja Mg. math. Laima Baltiņa, Jelgavas Tehnoloģiju vidusskolas matemātikas skolotāja

Iepriekšējā teorija

Atgriezties tēmā

Nākamā teorija

Nosūtīt atsauksmi

Atradi kļūdu?

Sūti mums ziņu!

Video mācību materiāli

"MATEMĀTIKA II"

PALĪGSMĀCĪBĀS.LV

10. Vienpusējas robežas definīcija

Teorija