Pētījumos dažreiz svarīgi noskaidrot, vai starp divām dažādām pazīmju vērtību kopām (variantēm) pastāv kāda sakarība. Piemēram, vai skolēna sekmes ir atkarīgas no tā, cik tālu viņš dzīvo no skolas, vai dzīvnieka masa ietekmē tā mūža garumu.
Divu vai vairāku datu kopu savstarpējo saistību raksturo korelācija.
Divu mainīgu lielumu sakarību sauc par korelatīvu, ja neatkarīgā mainīgā lieluma izmaiņas ir saistītas ar atkarīgā mainīgā lieluma vidējo vērtību izmaiņām.
Piemērs:
Izpētīsim, vai nedēļā pavadīto stundu skaits apmācības portālā Uzdevumi.lv un nopelnīto izcilo vērtējumu skaits ir savstarpēji saistīti lielumi - vai pastāv korelācija?
Dati ir apkopoti biežuma tabulā.
Dati ir apkopoti biežuma tabulā.
| Vārds | Rita | Atis | Vilis | Ella | Jānis | Ivo | Jana | Vita | Maija |
| Stundas | 2 | 3 | 4 | 5 | 6 | 3 | 7 | 7 | 8 |
Izcilo vērtējumu skaits | 3 | 2 | 5 | 3 | 6 | 4 | 7 | 5 | 8 |
Konstruējam korelācijas diagrammu.

Katrs punkts grafikā atbilst datiem par kādu konkrētu skolēnu.
Piemēram, Vita Uzdevumos.lv nedēļā vingrinās 7 stundas (punkta abscisa) un nopelnījusi 5 izcilus vērtējumus (punkta ordināta), punkts (7;5).
Starp abām pazīmēm pastāv korelācija, ja, atliekot abu pazīmju vērtībām atbilstošus punktus , tie izvietojas kādas iedomātas līnijas abās pusēs. Ja iedomātā līnija ir taisne, tad pastāv lineāra korelācija.
Taču, ja punkti ir pārāk izkliedēti (un šādu līniju novilkt nevar), tad atliek secināt, ka korelācija starp pazīmēm nepastāv.
1. attēls

Pozitīva lineāra korelācija (punkti novietojas ap iedomātu augošu taisni) - palielinoties vienas pazīmes vērtībai, palielinās otras pazīmes vērtības (1. attēls).
2. attēls

Negatīva lineāra korelācija (punkti novietojas ap iedomātu dilstošu taisni) - palielinoties vienas pazīmes vērtībai, samazinās otras pazīmes vērtības (2. attēls).
3. attēls

Korelācija nepastāv - vienas pazīmes izmaiņa neietekmē otras pazīmes vērtības izmaiņu (3 attēls).
Visbiežāk lietotais korelācijas raksturotājs ir Pīrsona korelācijas koeficients . Tas parāda, cik cieša ir divu pazīmju vērtību lineārā sakarība, proti, - cik cieši atliktie punkti izvietojas ap kādu iedomātu taisni.
Korelācijas koeficients .
Ciešāka ir tā sakarība, kurai korelācijas koeficients pēc moduļa ir lielāks.
Tiek uzskatīts, ka lineārā sakarība starp pazīmēm ir
- cieša, ja ;
- vidēja, ja ;
- vāja, ja ;
- kļūda aprēķinos, ja \(|r|>1\).
Diemžēl dažādos avotos korelācijas koeficienta \(r\) novērtējums atšķiras.
Korelācijas koeficientu \(r\) rēķina ar IT rīkiem.
Korelācijas koeficienta formula ir sarežģīta un tā nav jāprot:
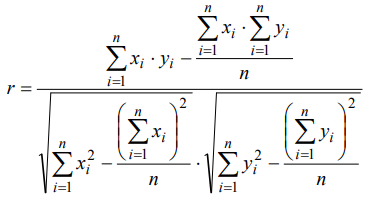
Papildmateriāls, kurā vari uzzināt vairāk par korelācijas diagrammām, korelācijas koeficientu un to attēlošanu izklājlapā Excel.
Atsauce:
Skola2030 mācību un metodiskie līdzekļi
Mācību video