Lineāru korelāciju var raksturot ar lineārās regresijas vienādojumu.
Vienkāršs pāru lineārās regresijas vienādojums vispārīgā veidā ir \(y=ax+b.\)
Regresijas vienādojumu var iegūt ar IT rīkiem.
Aplūkosim piemēru, kā atrast regresijas vienādojumu un korelācijas koeficientu datiem, kas doti Excel.
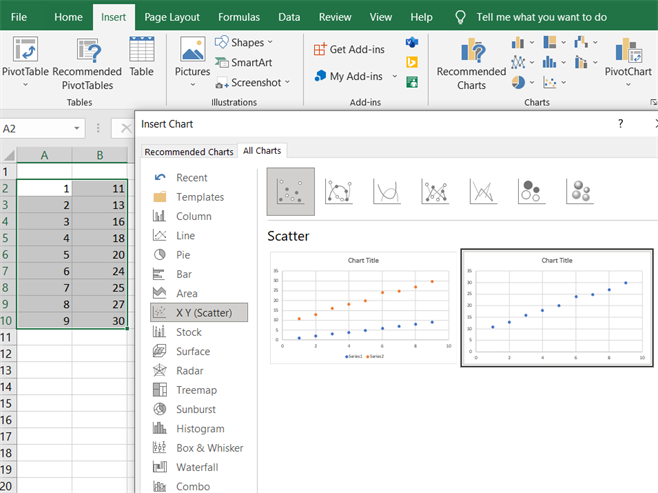
Vispirms iezīmē datus, tad izvēlas:
- Ievietošana (Insert);
- Ieteicamās diagrammas (Recommended Charts);
- Visas diagrammas (All Charts);
- XY izkliedes (Scatter);
- Izvēlamies diagrammu, kurā ir tikai punkti.
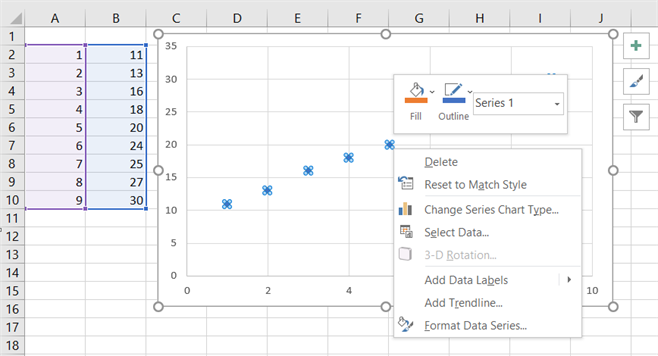
Lai iegūtu vienādojumu
- uzklikšķina uz datu vērtībām, tās iezīmējas kā krustiņi;
- uzspiežot ar labo klikšķi, var atrast izvēli: Pievienot tendences līkni (Add Trendline).
Labajā pusē atveras logs: Formatēt tendences (Format Trendline).
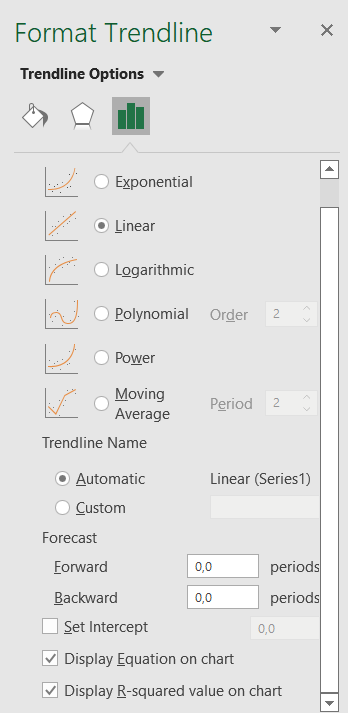
Parasti tiek piedāvāta izvēle: Lineāra funkcija (Linear).
Mums vēl nepieciešams izvēlēties:
- Rādīt vienādojumu diagrammā (Display Equation on chart).
- Rādīt R kvadrātā vērtību diagrammā (Display R-squared value on chart).
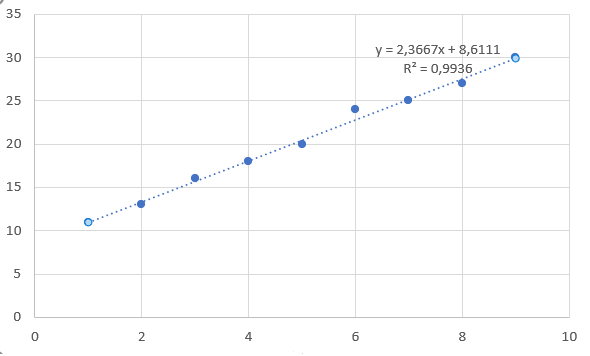
Iegūstam lineārās regresijas vienādojumu un korelācijas koeficienta \(r\) kvadrātu.
Lai uzzinātu \(r\), izvelk kvadrātsakni.
Varam secināt, ka abu datu kopu lineārā sakarība ir cieša.
Uzziņa
Atbilstību/ciešumu starp datiem un regresijas vienādojumu nosaka korelācijas (Pīrsona) koeficients \(r\). Korelācijas koeficients norāda lineārās sakarības ciešuma pakāpi.
\(0 < |𝑟| ≤ 0,25\) - ļoti vāja sakarība
\(0,25 < |𝑟| ≤ 0,5\) - vāja sakarība
\(0,5 < |𝑟| ≤ 0,75\) - vidēja sakarība
\(0,75 < |𝑟| ≤ 1\) - cieša sakarība
\(|r|>1\) - nepareizi aprēķini
Vingrinies šīs tēmas 17. uzdevumu! Izpēti atbilžu soļus!
Atsauce:
Materiālu sagatavoja Mg. math. Laima Baltiņa
Skola2030 kursu materiāli