1. Parabola, tās vienādojums

 

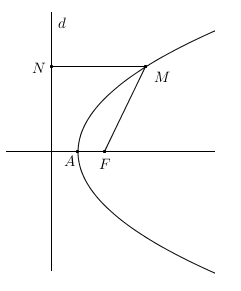
Parabolas simetrijas asi sauc par parabolas asi. Punktu, kurā parabola krusto savu asi, sauc par parabolas virsotni (zīmējumā punkts A).

 

 

Lai iegūtu parabolas vienādojumu, novietosim parabolu tā, lai Ox ass ietu cauru fokusam perpendikulāri direktrisei, bet koordinātu sākumpunktu novietosim pa vidu starp direktrisi un fokusu.

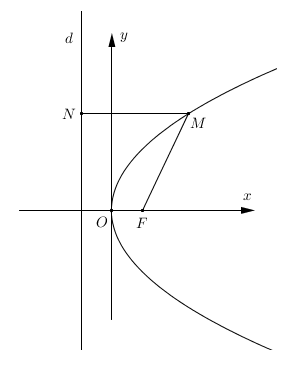
Apzīmēsim attālumu starp direktrisi un fokusu ar p. Tā kā parabolas virsotne ir tieši pa vidu starp fokusu un direktrisi, tad fokusa koordinātas ir $F\left(\frac{p}{2};0\right)$, bet direktrises vienādojums ir $x=-\frac{p}{2}$.

Tad punkta $M\left(x;y\right)$ attālums līdz fokusam ir $\mathit{FM}=\sqrt{{\left(x-\frac{p}{2}\right)}^2+y^2}$, bet attālums līdz direktrisei - $\mathit{MN}=x+\frac{p}{2}$.

Abiem attālumiem jābūt vienādiem, tāpēc $\sqrt{{\left(x-\frac{p}{2}\right)}^2+y^2}=x+\frac{p}{2}$.

Pēc nelielas vienkāršošanas: