1. Vispārīgais vienādojums

 

 

Brīvi izvēlēsimies taisni $l$. Tad nofiksēsim kādu šīs taisnes punktu $M_0$ un kādu tai perpendikulāru nenulles vektoru $\overrightarrow{n}$. Ja M ir brīvi izvēlēts šīs taisnes punkts (kas nav $M_0$), tad vektori $\overrightarrow{M_{0}M}$ un $\overrightarrow{n}$ ir perpendikulāri un tātad to skalārais reizinājums ir 0: $\left(\overrightarrow{n},\overrightarrow{M_{0}M}\right)=0$.

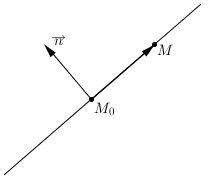
Ja $\overrightarrow{n}=\left(A;B\right)$, $M_0\left(x_0;y_0\right)$ un $M\left(x;y\right)$, tad $\overrightarrow{M_{0}M}=\left(x-x_0;y-y_0\right)$ un var izteikt skalāro reizinājumu ar koordinātām: $A\left(x-x_0\right)+B\left(y-y_0\right)=0$ jeb $\mathit{Ax}+\mathit{By}-A{x}_0-B{y}_0=0$. Apzīmējot izteiksmi $-A{x}_0-B{y}_0$ ar C, iegūstam taisnes vispārīgo vienādojumu $\mathit{Ax}+\mathit{By}+C=0$.

 

 

Ja dots vienādojums $\mathit{Ax}+\mathit{By}+C=0$, paņemsim kādu punktu $\left(x_0,y_0\right)$, kura koordinātas ir šī vienādojuma risinājums. Tad $A{x}_0+B{y}_0+C=0$ jeb $C=-A{x}_0-B{y}_0$ un vienādojumu var pārrakstīt kā $\mathit{Ax}+\mathit{By}-A{x}_0-B{y}_0=0$.

Bet tas, kā iepriekš noskaidrojām, ir vienādojums taisnei, ja dots tās punkts $M_0\left(x_0;y_0\right)$ un taisnei perpendikulārs vektors $\overrightarrow{n}=\left(A;B\right)$.