Ja taisnes vispārīgajā vienādojumā koeficients \(B\) atšķiras no \(0\), tad var izteikt \(y\) vērtību: .
Apzīmējot un , iegūst vienādojumu .
Taisnes vienādojumu sauc par taisnes vienādojumu ar virziena koeficientu.
Noskaidrosim koeficientu \(k\) un \(b\) ģeometrisko nozīmi.
Ja ņem divus dažādus taisnes punktus un , kuriem , tad no divām vienādībām un var izteikt \(k\) vērtību: .
Ja \(k\) vērtība ir pozitīva, tad un , kur ir leņķis, ko taisne veido ar \(Ox\) ass pozitīvo virzienu. (Skatīt zīmējumu.)
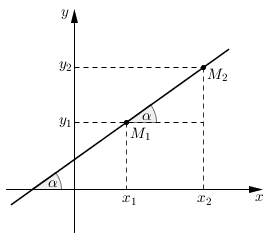
Ja k vērtība ir negatīva, tad . Šeit , attiecīgi .
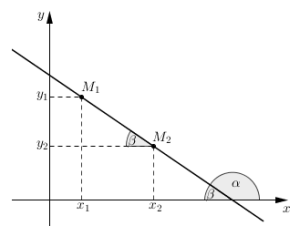
Un, protams, ja , tad taisne ir paralēla \(Ox\) asij, un atkal .
Vispārinot no šiem gadījumiem, sanāk šāda koeficienta \(k\) ģeometriskā nozīme:
Svarīgi!
Koeficienta \(k\) vērtība ir vienāda ar tangensu no leņķa starp \(Ox\) asi un taisni, ja leņķi mēra no \(Ox\) ass pozitīvā virziena un pulksteņrādītāja virzienā.
Ar koeficientu \(b\) ir vienkārši. Ja taisnes vienādojumā ievieto vērtību , tad . Tātad:
Svarīgi!
Koeficients \(b\) norāda taisnes punkta ordinātu (\(y\) koordinātu), ja tā abscisa (\(x\) koordināta) ir \(0\).