2. Ģeometriskā interpretācija

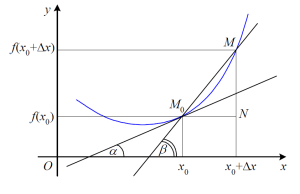
Caur līnijas punktiem $M_0$ un M novilksim taisni $M_{0}M$. Šo taisni sauc par sekanti. Ar $\mathrm{\beta }$ apzīmēsim leņķi, ko šī sekante veido ar \(Ox\) ass pozitīvo virzienu. Pieņemsim, ka punkts M pārvietojas pa līniju, tuvojoties punktam $M_0$, kurš ir nekustīgs. Tādā gadījumā arī sekante mainās. Punktam M, nonākot punktā $M_0$, sekante $M_{0}M$ kļūst par līnijas pieskari punktā $M_0$. Pieņemsim, ka pieskare ar \(Ox\) asi veido leņķi $\mathrm{\alpha }$.

Apskatīsim taisnleņķa trijstūri $M_0\mathit{MN}$. Šajā trijstūrī leņķis ${\mathit{MM}}_{0}N$ = $\mathrm{\beta }$, piekatete $M_{0}N$ sakrīt ar argumenta pieaugumu, t.i., $M_{0}N$ = $\mathrm{\Delta }$x, pretkatete \(MN\) sakrīt ar funkcijas pieaugumu, t.i., \(MN\) = $\mathrm{\Delta }$y. No sakarībām taisnleņķa trijstūrī seko, ka

$\mathit{tg}\mathrm{\beta }=\frac{\mathit{MN}}{M_{0}N}=\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}$

Ja $\mathrm{\Delta }x\to 0$, tad punkts $M\to M_0$, sekante $M_{0}M\to$pieskare punktā $M_0$, $\mathrm{\beta }\to \mathrm{\alpha },\mathit{tg}\mathrm{\beta }\to \mathit{tg}\mathrm{\alpha }$ jeb

$\mathit{tg}\mathrm{\alpha }=\underset{\mathrm{\Delta }x\to 0}{\mathit{lim}}\mathit{tg}\mathrm{\beta }=\underset{\mathrm{\Delta }x\to 0}{\mathit{lim}}\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}=f^{\prime }\left(x_0\right)$

No analītiskās ģeometrijas kursa zināms, ka tangenss leņķim, ko taisne veido ar \(Ox\) asi, ir vienāds ar taisnes virziena koeficientu. Tātad funkcijas grafikam punktā $M_0\left(x_0,f\left(x_0\right)\right)$ vilktās pieskares virziena koeficients sakrīt ar šīs funkcijas atvasinājumu punktā $x_0$:

$k_p=\mathit{tg}\mathrm{\alpha }=f^{\prime }\left(x_0\right)$

Tā ir atvasinājuma ģeometriskā interpretācija.

Kā zināms no analītiskās ģeometrijas kursa, vienādojums taisnei, kas iet caur punktu $M_0\left(x_0,f\left(x_0\right)\right)$ un kuras virziena koeficients ir \(k\), ir

$y-f\left(x_0\right)=k\left(x-x_0\right)\mathit{jeb}y=f\left(x_0\right)+k({x-x}_0)$.