Vektoru starpība — teorija. Matemātika, Augstskola: 1. kurss.

Par divu vektoru

\vec{a}

\vec{b}

starpību

\vec{a} - \vec{b}

sauc tādu vektoru

\vec{c}

, ka

\vec{b} + \vec{c} = \vec{a}

Lai iegūtu divu vektoru starpību, var izmantot trijstūra likumu:

Vektoru

\vec{a}

\vec{b}

starpība ir vienāda ar vektoru, kas novilkts no vektora

\vec{b}

galapunkta uz vektora

\vec{a}

galapunktu, ja abi šie vektori atlikti no viena punkta.

Bet var arī pieskaitīt pretēju vektoru, kas ir vienkāršāka un vieglāk iegaumējama metode:

Vektoru

\vec{a}

\vec{b}

starpība ir vienāda ar vektora

\vec{a}

un vektoram

\vec{b}

pretējā vektora summu:

\vec{a} - \vec{b} = \vec{a} + (- \vec{b})

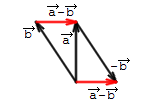
Piemērs:

1) Jāvienkāršo izteiksme starpība

\vec{AB} - \vec{CB}

. Lai to izdarītu, vektora

\vec{CB}

atņemšanu aizvieto ar tam pretējā vektora

\vec{BC}

pieskaitīšanu un tad saskaita pēc trijstūra likuma:

\vec{AB} - \vec{CB} = \vec{AB} + \vec{BC} = \vec{AC}

Piemērs:

2) Dots paralēlskaldnis (zīmējumā). Jāvienkāršo izteiksme

\vec{A_{1} B_{1}} - \vec{BC} + \vec{D D_{1}}

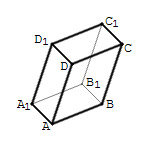
Vispirms vektora atņemšanu pārveido par tam pretējā vektora pieskaitīšanu:

\vec{A_{1} B_{1}} - \vec{BC} + \vec{D D_{1}} = \vec{A_{1} B_{1}} + \vec{CB} + \vec{D D_{1}}

Tālāk izmanto to, ka

\vec{A_{1} B_{1}} = \vec{DC}

\vec{D D_{1}} = \vec{B B_{1}}

. Pēc šādas aizvietošanas var viegli saskaitīt, izmantojot daudzstūra likumu:

\vec{A_{1} B_{1}} + \vec{CB} + \vec{D D_{1}} = \vec{DC} + \vec{CB} + \vec{B B_{1}} = \vec{D B_{1}}

Rezultāts:

\vec{A_{1} B_{1}} - \vec{BC} + \vec{D D_{1}} = \vec{D B_{1}}

Atradi kļūdu?

4. Vektoru starpība