Funkcijas paritāte — teorija. Matemātika, 10. klase.

ONLINE VIDEO KURSS

"MATEMĀTIKA 10. KLASEI"

Pāra un nepāra funkcijas

Funkciju \(y = f(x)\) sauc par pāra funkciju, ja visiem \(x\) no definīcijas apgabala \(f(-x) = f(x)\).

Pāra funkcijas grafiks ir simetrisks pret \(Oy\) asi (skat. 1. zīm.)

Funkciju \(y = f(x)\) sauc par nepāra funkciju, ja visiem \(x\) no definīcijas apgabala \(f(-x) = - f(x)\).

Nepāra funkcijas grafiks ir centrāli simetrisks pret koordinātu sākumpunktu \((0;0)\) (skat. 2. zīm.)

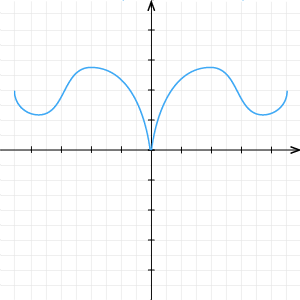1. zīm. Pāra funkcija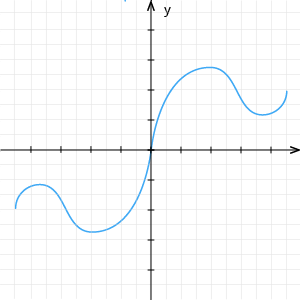

2. zīm. Nepāra funkcija

Parasti gan funkcija nav ne pāra, ne nepāra.

Pēc grafika var redzēt, ka pāra funkcija ir, piemēram, kvadrātfunkcija

y = x^{2} - 2

(skat. 3. zīm.), bet ne pāra, ne nepāra ir kvadrātfunkcija

y = x^{2} - 2 x - 1

(skat 4. zīm.)

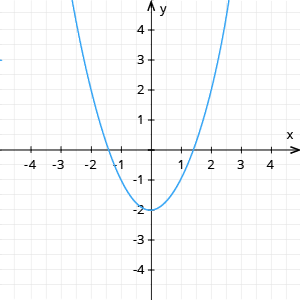3. zīm. Pāra funkcija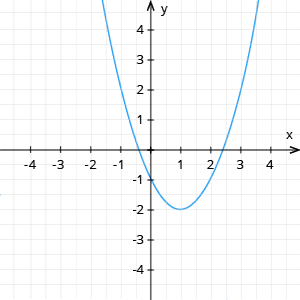

4. zīm. Ne pāra, ne nepāra funkcija

Nepāra funkcijas ir, piemēram,

y = - \frac{1}{x}

(5. zīm.) un \(y=x^3\) (6. zīm.).

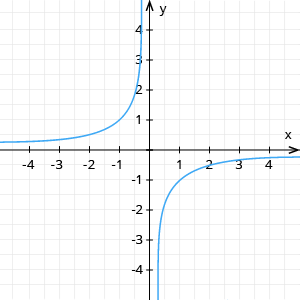5. zīm. Nepāra funkcija

6. zīm. Nepāra funkcija

Svarīgi!

Ja funkcija \(f(x)\) uzdota analītiski (ar formulu), tad, lai pārbaudītu funkcijas paritāti, jārēķina funkcijas vērtība \(f(-x)\).

Piemērs:

Nosaki dotās funkcijas paritāti!

\begin{array}{l} f (x) = x^{3} - x \\ f (- x) = {(- x)}^{3} - (- x) = - x^{3} + x \end{array}

Redzam, ka iegūtā funkcija nav vienāda ar doto funkciju - \(f(-x)\) nav vienāda ar \(f(x)\), tātad funkcija nav pāra.

Lai pārbaudītu, vai funkcija ir nepāra, iznes pirms iekavām mīnus zīmi:

f (- x) = {(- x)}^{3} - (- x) = - x^{3} + x = - (x^{3} - x) = - f (x)

.

Redzam, ka funkcija ir nepāra jo \(f(-x) = -f(x)\).

Atradi kļūdu?

ONLINE VIDEO KURSS

"MATEMĀTIKA 10. KLASEI"

2. Funkcijas paritāte