OTRĀ SEMESTRA NOSLĒGUMA TESTI
Funkciju, kuras vispārīgais veids ir , kur \(a\), \(b\), \(c\) ir reāli skaitļi, \(a \neq 0\), sauc par kvadrātfunkciju.
Definīcijas apgabals \(D(f)\) ir visi reālie skaitļi.
Vērtību apgabalu \(E(f)\) nolasa no grafika, tas ir atkarīgs no parabolas virsotnes \(y\) koordinātas un no zaru vērsuma.
- 1. piemērā ;
- 2. piemērā .
Svarīgi!
Parametrs \(a\) nosaka zaru vērsumu:
ja \(a > 0\), tad zari ir uz augšu (skat 1. piem.)
ja \(a < 0\), tad zari ir uz leju (skat 2. piem.)
Parametrs \(c\) norāda, kurā punktā parabola krusto \(y\) asi.
ja \(a > 0\), tad zari ir uz augšu (skat 1. piem.)
ja \(a < 0\), tad zari ir uz leju (skat 2. piem.)
Parametrs \(c\) norāda, kurā punktā parabola krusto \(y\) asi.
Lai konstruētu kvadrātfunkcijas grafiku:
- aprēķina parabolas virsotnes koordinātas: un \(y_o\), kuru iegūst, ievietojot funkcijā;
- atliek virsotni koordinātu plaknē, novelk parabolas simetrijas asi;
- nosaka zaru vērsumu;
- atliek krustpunktu ar \(y\) asi;
- un tikai tad sastāda vērtību tabulu.
Atrisinot kvadrātvienādojumu , iegūst krustpunktus ar \(Ox\) asi jeb funkcijas nulles (saknes) (ja diskriminants \(D>0\)):
- ja \(D < 0\) tad, krustpunktu ar \(x\) asi nav,
- ja \(D = 0\), tad parabolas virsotne atrodas uz \(x\) ass.
Piemērs:
Konstruē grafiku .
Zaru vērsums uz augšu, jo \(a = 1 > 0\). \(Oy\) asi krusto punktā \((0; -1)\).
Simetriski piezīmē parabolas kreiso pusi. | 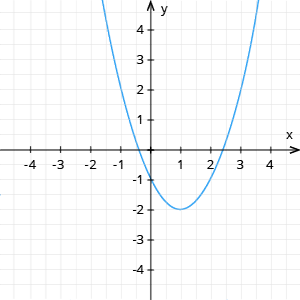 |
Kvadrātfunkcijas virsotnes abscisu var noteikt arī izmantojot funkcijas saknes:
Piemērs:
Nosaki kvadrātfunkcijas virsotnes koordinātas!
Redzam, ka šai funkcijai ir viegli aprēķināt saknes. Izmantosim to. Ja ir zināmas saknes, tad virsotnes koordinātas ir | 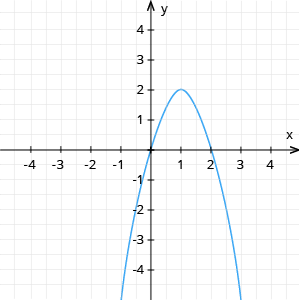 |