Trijstūris un riņķis — teorija. Matemātika, 10. klase.

ONLINE VIDEO KURSS

"MATEMĀTIKA 10. KLASEI"

Riņķa līniju var ievilkt un to var apvilkt ap jebkuru trijstūri.

Trijstūrī ievilktas riņķa līnijas centrs ir bisektrišu krustpunkts.

Trijstūrim apvilktas riņķa līnijas centrs ir trijstūra malu vidusperpendikulu krustpunkts.

Formulas

Ievilkts vienādmalu trijstūris	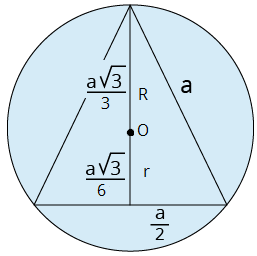Vienādmalu trijstūrī ievilktas riņķa līnijas rādiuss $r = \frac{1}{3} h$ , kur $h$ ir trijstūra augstums. Ja dota trijstūra mala $a$, tad $h = \frac{a \sqrt{3}}{2}$ Tātad $r = \frac{a \sqrt{3}}{6}$ (dots formulu lapā) Apvilktas riņķa līnijas rādiuss $R = \frac{2}{3} h$ , kur $h$ ir trijstūra augstums. Ja dota trijstūra mala $a$, tad $R = \frac{a \sqrt{3}}{3}$ (dots formulu lapā)
Ievilkts taisnleņķa trijstūris	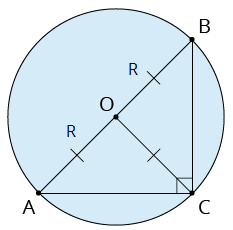Trijstūrī ievilktas riņķa līnijas rādiuss $r = \frac{S_{Δ}}{p}$ , kur $p$ - pusperimetrs Taisnleņķa trijstūrim apvilktas riņķa līnijas rādiuss $R = \frac{c}{2}$ , kur $c$ - hipotenūza.
Patvaļīgs trijstūris 1) Ievilkts šaurleņķa trijstūris 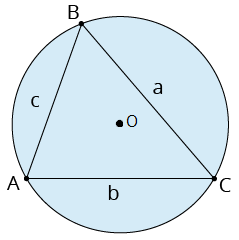2) Ievilkts platleņķa trijstūris	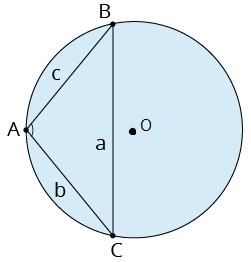Patvaļīgā trijstūrī ievilktas riņķa līnijas rādiuss $r = \frac{S_{Δ}}{p}$ , kur $p$ - pusperimetrs Patvaļīgam trijstūrim apvilktas riņķa līnijas rādiuss $R = \frac{a \cdot b \cdot c}{4 \cdot S_{Δ}}$ $R = \frac{a}{2 \sin α}$ , $α$ ir malas $a$ pretleņķis (no sinusu teorēmas)