Eksponentfunkcijas definīcija un īpašības — teorija. Matemātika, 12. klase.

Video mācību materiāli

"MATEMĀTIKA II"

Funkciju

y = a^{x}

, kur

a

ir pozitīvs reāls skaitlis (

a > 0

a \neq 1

), sauc par eksponentfunkciju.

Eksponentfunkcija ir definēta visām reālām

x

vērtībām:

D (y) = ℝ

Vērtību apgabals ir

E (y) = (0; + \infty)

Lai konstruētu eksponentfunkcijas grafiku, sastāda tabulu. Tabulā izvēlas gan negatīvas, gan pozitīvas

x

vērtības.

Piemērs:

Konstruē eksponentfunkciju grafikus.

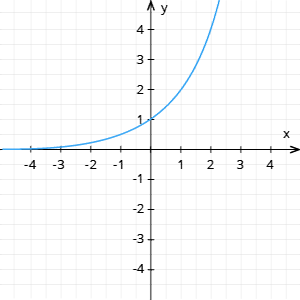
(1. zīm.)

y = 2^{x}

$x$	−2	−1	0	1	2	3
$y$	$\frac{1}{4}$	$\frac{1}{2}$	1	2	4	8

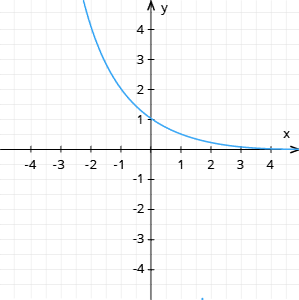
(2. zīm.)

y = {0,5}^{x}

$x$	−3	−2	−1	0	1	2
$y$	8	4	2	1	$\frac{1}{2}$	$\frac{1}{4}$

Funkcija nekrusto

x

asi, bet bezgalīgi tuvojas tai.

Funkcijas

y = a^{x}

grafiks krusto

y

asi punktā

(0; 1)

Svarīgi!

Funkcijas augšana un dilšana ir atkarīga no parametra

a

vērtības:
1) ja

a > 1

, tad funkcija aug visām

x

vērtībām (skat. 1. zīm.)
2) ja

0 < a < 1

, tad funkcija dilst visām

x

vērtībām (skat 2. zīm.).

Šo īpašību izmanto eksponentnevienādību atrisināšanā.

Eksponentfunkcijai nav ne lielākās, ne mazākās vērtības, tā nav ne pāra, ne nepāra funkcija.

Atradi kļūdu?

Video mācību materiāli

"MATEMĀTIKA II"

1. Eksponentfunkcijas definīcija un īpašības