Par funkcijas \(y=f(x)\) nullēm sauc tās argumenta \(x\) vērtības, ar kurām funkcijas vērtība vienāda ar nulli.
Ja dota funkcijas analītiskā izteiksme (formula), funkcijas nulles var iegūt, atrisinot vienādojumu \(f(x)=0\).
Piemērs:
Dota lineāra funkcija \(y=2x-4\). Nosaki funkcijas nulles!
Risina vienādojumu \(2x-4=0\)
\(2x=4\)
\(x=2\)
Atbilde. Funkcijas nulle ir \(x=2\).
Ja ir noteiktas funkcijas nulles, var noteikt vienādzīmju intervālus.
Vienādzīmju intervāli ir tie intervāli, kuros funkcijas vērtības ir ar vienādām zīmēm- tikai pozitīvas vai tikai negatīvas.
Intervālā starp divām blakus esošām funkcijas nullēm funkcija ir vai nu pozitīva \(f(x)>0\), vai arī negatīva \(f(x)<0\).
Risina attiecīgo nevienādību.
Piemērs:
Dota lineāra funkcija \(y=2x-4\). Nosaki tās argumenta vērtības, ar kurām \(y<0\)!
Risina nevienādību \(2x-4<0\)
\(2x<4\)
\(x<2\)
Atbilde.
Piemērs:
Dota kvadrātfunkcija . Nosaki tās argumenta vērtības, ar kurām funkcija ir pozitīva!
Tātad jānosaka tās \(x\) vērtības, ar kurām \(y>0\).
1. aprēķina kvadrātvienādojuma saknes:
2. skicē parabolu, atzīmē pozitīvās vētības:
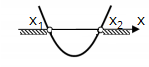
Atbilde. Funkcija ir pozitīva, ja .