Taisnu prizmu, kuras pamats ir taisnstūris, sauc par taisnstūra paralēlskaldni.
Trīs šķautnes, kas iziet no vienas un tās pašas taisnstūra paralēlskaldņa virsotnes, sauc par dimensijām.
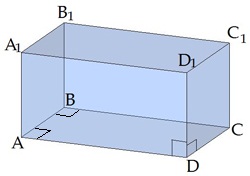
Šajā piemērā trīs dimensijas ir šķautnes
Taisnstūra paralēlskaldņa diagonāles garuma kvadrāts ir vienāds ar triju dimensiju garumu kvadrātu summu:
, kur , , ir dimensijas jeb platums, garums un augstums.
(Līdzīgi kā Pitagora teorēma, tikai klāt nāk trešā dimensija.)
Zīmējumā sanāk
Svarīgi!
Atceries, ka taisnstūra paralēlskaldnī visas diagonāles ir vienāda garuma:
Kuba diagonāļu formula
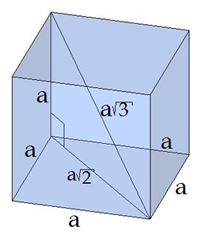
Tā kā kubam visu dimensiju garumi ir vienādi, apzīmēsim ar , tad .
No abām pusēm izvelkot sakni, iegūst kuba diagonāles formulu: