Funkciju, kuras vispārīgais veids ir \(y = kx + b\), kur , sauc par lineāru funkciju.
Koeficientu \(k\) sauc par lineārās funkcijas grafika virziena koeficientu. Tā kā lineāras funkcijas grafiks ir taisne, tad var teikt, ka \(k\) ir atbilstošās taisnes virziena koeficients.
Taisnes virziena koeficienta ģeometriskā jēga:
, kur ir leņķis, ko veido funkcijas grafiks ar \(Ox\) ass pozitīvo virzienu.
Funkcijas pieauguma un argumenta pieauguma attiecība ir vienāda ar koeficienta \(k\) vērtību.
Piemērs:
Nosaki attēlā redzamās lineārās funkcijas \(y=kx+b\) virziena koeficientu!
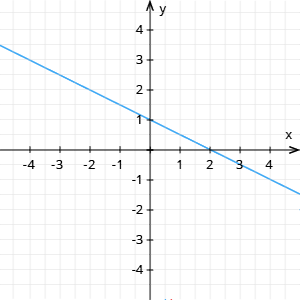
Uz \(Ox\) ass izvēlas un , iegūst argumenta pieaugumu
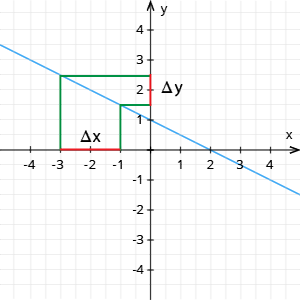
Atrod atbilstošos un , iegūst atbilstošo funkcijas pieaugumu