y = cos x grafiks un tā īpašības — teorija. Matemātika, 12. klase.

Lai uzzīmētu funkcijas \(y = \cos x\) grafiku, sastāda vērtību tabulu, izvēlas vienības uz koordinātu asīm (skat. teoriju "Koordinātu plakne trigonometrisko funkciju konstruēšanai").

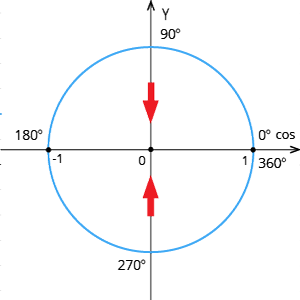
Īpaši svarīgi ir pareizi atlikt kosinusa vērtības, kuras var precīzi nolasīt no vienības riņķa:

\(\cos 0°=1\)

\(\cos 90°=0\)

\(\cos 180°=-1\)

\(\cos 270°=0\)

\(\cos 360°=1\)

Asset 21.svg

Funkcijas \(y = \cos x\) īpašības:

Īpašības var noteikt gan no vienības riņķa, gan no funkcijas grafika.

Funkcijas definīcijas apgabals \(D(y) = \) $(- \infty; + \infty)$ .
Funkcijas \(y = \cos x\) vērtību apgabals \(E(y) = [-1; 1].\)
Funkcija \(y = \cos x\) ir pāra funkcija, t.i., \(cos(-x) =cos\ x.\)
Periodiska funkcija ar periodu $2 π$ , t.i., \(\cos(x+2\pi n) = \cos x\), kur $n \in ℤ$ .
Krustpunkti ar \(Ox\) asi (funkcijas nulles) ir punkti, kuriem $x = \frac{π}{2} + π n$ , kur $n \in ℤ$ .
Krustpunkts ar \(Oy\) asi ir punkts \((0; 1)\).
Pozitīva I un IV kvadrantā, t.i., ja $x \in (- \frac{π}{2} + 2 π n; \frac{π}{2} + 2 π n)$ , kur $n \in ℤ$ .
Negatīva II un III kvadrantā, t.i., ja $x \in (\frac{π}{2} + 2 π n; \frac{3 π}{2} + 2 π n)$ , kur $n \in ℤ$ .
Augoša III un IV kvadrantā, t.i., ja $x \in (- π + 2 π n; 2 π n)$ , kur $n \in ℤ$ .
Dilstoša I un II kvadrantā, t.i., ja $x \in (2 π n; π + 2 π n)$ , kur $n \in ℤ$ .
Maksimuma punkti: \(y = 1\), ja $x = 0 + 2 π n$ , kur $n \in ℤ$ .
Minimuma punkti: \(y = -1\), ja $x = π + 2 π n$ , kur $n \in ℤ$ .
Nepārtraukta funkcija.

Iepriekšējā teorija

Atgriezties tēmā

Nākamā teorija

Nosūtīt atsauksmi

Atradi kļūdu?

Sūti mums ziņu!