Skaitli, kas izsaka, par cik viens skaitlis lielāks nekā otrs, sauc par abu skaitļu starpību.
Skaitli, kurš izsaka, cik reižu viens skaitlis ir lielāks nekā otrs, sauc par abu skaitļu attiecību.
Piemēram, ja nogrieznis \(AB\) ir \(3\) reizes garāks par nogriezni \(MK\), tad nogriežņu \(AB\) un \(MK\) attiecība ir \(3\) jeb \(AB : MK = 3\).
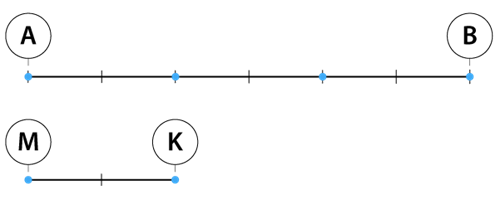
Attiecību var pierakstīt ar diviem skaitļiem.
Pieņemot īsākā nogriežņa (\(MK\)) garumu par \(1\) vienību, nogriežņa \(AB\) garums ir \(3\) tādas vienības.
Var uzrakstīt: \(AB:MK=3:1\).
To lasa: \(AB\) un \(MK\) attiecība ir \(3\) pret \(1\) jeb \(AB\) attiecas pret \(MK\) kā \(3\) pret \(1\).
Var rakstīt arī otrādi: \(MK:AB = 1:3\) (lasa - \(MK\) attiecas pret \(AB\) kā \(1\) pret \(3\)).
Par divu skaitļu attiecību sauc abu skaitļu dalījumu.
Piemēram, skaitļu \(20\) un \(4\) attiecība ir \(5\), jo \(20:4=5\). Tas izsaka, ka \(20\) ir \(5\) reizes lielāks nekā \(4\).
Dalījums \(20:4\) ir attiecības izteiksme, bet dalījums \(5\) ir attiecības vērtība.
Attiecības jēdzienu lieto skaitļu salīdzināšanai, lai noskaidrotu, cik reižu viens skaitlis ir lielāks par otru skaitli.
Ar attiecību var salīdzināt tikai viena un tā paša lieluma skaitliskās vērtības, piemēram, cik ir \(4\) m un \(20\) cm attiecība. Nevar aprēķināt, cik ir \(4\) kg un \(20\) cm attiecība, šādai salīdzināšanai nav jēgas.

