OTRĀ SEMESTRA NOSLĒGUMA TESTI
Lai labāk saprastu, kas ir divu skaitļu attiecība, aplūkosim piemēru ar nogriežņiem.
Doti divi nogriežņi AB un VN
Vai vari noteikt, cik reižu pirmais ir garāks par otro?
Abus garumus var salīdzināt, dalot vienu ar otru.
20 m : 10 m = 2
Šis dalījums rāda, ka pirmais nogrieznis ir 2 reizes garāks nekā otrs.
Citiem vārdiem, pirmā nogriežņa un otrā nogriežņa attiecība ir 2.
Turpretim dalījums rāda, ka otrā nogriežņa garums ir no pirmā nogriežņa garuma.
Par divu skaitļu attiecību sauc šo skaitļu dalījumu.
Dalot lielāko skaitli ar mazāko, uzzina, cik reižu viens skaitlis ir lielāks nekā otrs.
Dalot mazāko skaitli ar lielāko, uzzina, kāda daļa ir viens skaitlis attiecībā pret otru.
Par divu skaitļu attiecību dažkārt sauc arī vēl neaprēķinātu dalījumu.
Tā, piemēram, var uzrakstīt, ka
otrā nogriežņa un pirmā nogriežņa garumu attiecība ir 1 pret 2 (raksta 1 : 2).
VN : AB = 1 : 2.
Arī sporta spēlēs iegūto punktu attiecību pieņemts izteikt kā vēl neizrēķinātu dalījumu.
Piemēram, ja "Dinamo" iesituši 8 vārtus, bet pretinieku komanda "Ziķeri" - 2 vārtus,
tad spēles rezultāts ir 8 : 2.
Šo attiecību izrēķinot, atrodam skaitli 4. Tas rāda, ka "Dinamo" iesituši 4 reizes vairāk vārtu nekā "Ziķeri".
Skaitļu attiecību izmanto arī kartes mēroga pierakstīšanā.
Dalāmo un dalītāju mēdz saukt par attiecības locekļiem:
dalāmais ir pirmais loceklis,
bet dalītājs - otrais loceklis.
Piemērs:
Ko nozīmē, ka divu skaitļu attiecība 3 : 18 ?
Tas nozīmē, ka pirmais skaitlis ir 6 reizes (18 : 3 = 6) mazāks par otro skaitli, bet otrais skaitlis ir 6 reizes lielāks par pirmo skaitli.
Piemērs:
Aplūkosim nogriežņus AR un VZ
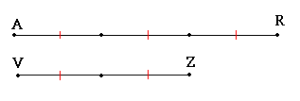
Šajā piemērā nogrieznis AR ir trīs vienības, bet VZ ir divas vienības garš.
Nogriežņu VZ un AR attiecība ir 2 : 3
Var pierakstīt VZ : AR = 2 : 3 jeb
Skaitļu attiecība šajā piemērā ir noderīga, jo būtu neiespējami atbildēt uz jautājumu: cik reižu otrais nogrieznis ir īsāks par pirmo, jo pirmo attiecības locekli (2) ar otro locekli (3) nevar izdalīt.