Trijstūri, kvadrātu, riņķi un citas figūras var uzzīmēt uz papīra, tātad plaknē. Taču matemātikā mācās arī par tādām figūrām, kas neatrodas plaknē.
Attēlā ir redzamas dažādu izmēru kastes. Līdzīga forma ir arī ķieģelim, istabai, datora monitoram.

Šāda veida ģeometrisku ķermeni matemātikā sauc par taisnstūra paralēlskaldni.
Taisnstūra paralēlskaldni no visām pusēm ierobežo taisnstūri.
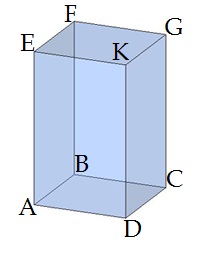
Šos sauc par taisnstūra paralēlskaldņa skaldnēm.
Attēlā skaldnes ir, piemēram, taisnstūri \(ABCD\), \(AEKD\).
Šo taisnstūru malas sauc par taisnstūra paralēlskaldņa šķautnēm.
Attēlā šķautnes ir, piemēram nogriežņi \(AD\) un \(DK\).
Taisnstūru virsotnes sauc par taisnstūra paralēlskaldņa virsotnēm.
Attēlā virsotnes ir, piemēram, \(A\) un \(G.\)
Taisnstūra paralēlskaldņa izmēru nosaka trīs šķautņu, kas iziet no vienas virsotnes, garumi.
Šo šķautņu garumus sauc par platumu, garumu un augstumu. Vienā vārdā tās sauc par dimensijām.
Attēlā platums, garums un augstums ir, piemēram, \( DA\), \(DC\) un \(DK\).
Ja taisnstūra paralēlskaldnim visas skaldnes ir kvadrāti, tad šādu ģeometrisko ķermeni sauc par kubu.
Kubs ir, piemēram, spēļu kauliņš. Skat. attēlā.

Attēlā dots kubs \(ABCDEFGK.\)
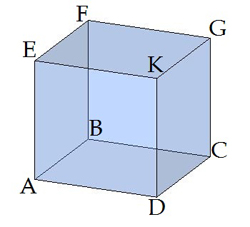
Kubam visas trīs dimensijas (platums, garums un augstums) ir vienādas. Tātad \(AD=DC=DK\).

