Centrālā simetrija
"Divus punktus sauc par simetriskiem attiecībā pret punktu O, ja punkts O atrodas uz nogriežņa, kas savieno šos punktus, un punkts O ir šī nogriežņa viduspunkts."
"Punktu O sauc par simetrijas centru, bet pašus punktus - par centrāli simetriskiem attiecībā pret punktu O."
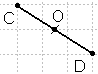 |  |
CO = DO, O - simetrijas centrs, C un D ir simetriski attiecībā pret punktu O.
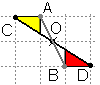
AO = BO, O - simetrijas centrs, A un B ir simetriski attiecībā pret punktu O.
Dzeltenā figūra (F1) un sarkanā figūra (F2) ir simetriskas attiecībā pret punktu O.
Dzeltenā figūra (F1) un sarkanā figūra (F2) ir simetriskas attiecībā pret punktu O.
"Figūras F1 un F2 sauc par simetriskām attiecībā pret kādu punktu, ja katram figūras F1 punktam eksistē simetrisks punkts figūrā F2 un otrādi."
Svarīgi!
Centrālā simetrija ir simetrija pret punktu.
Centrāli simetriskās figūrās atbilstošie figūru elementi ir vienādi. Centrālajā simetrijā saglabājas attālumi.
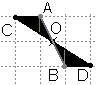
Dotajā piemērā
1) nogrieznis attēlojas par tam vienādu nogriezni (CO = DO, AO = BO, AC = BD).
2) leņķis attēlojas par tam vienādu leņķi .
Secinājums: figūra attēlojas par tai vienādu figūru .
Secinājums: figūra attēlojas par tai vienādu figūru .
Lai uzzīmētu punktam A simetrisku punktu D attiecībā pret simetrijas centru O:
1) plaknē atliek punktus A un O;
2) velk staru AO;  | 3) uz stara AO atliek punktu D, tā lai AO = OD.  |