Izmantojot romba pazīmes, var noteikt, vai četrstūris ir rombs.
Piemērs:
Mēģini atbildēt uz jautājumu: ja četrstūra diagonāles krustpunktā veido \(90\) grādu leņķi, vai tas noteikti ir rombs?
Izrādās, ka nav, jo tas var būt arī deltoīds (pūķis) vai kāds cits četrstūris, kam nav nosaukuma.
Izrādās, ka nav, jo tas var būt arī deltoīds (pūķis) vai kāds cits četrstūris, kam nav nosaukuma.
Lai četrstūris būtu rombs, bieži vien vispirms ir jāpierāda, ka četrstūris ir paralelograms. Tātad jāzina paralelograma pazīmes.
1. Ja paralelograma diagonāles ir perpendikulāras, tad tas ir rombs.
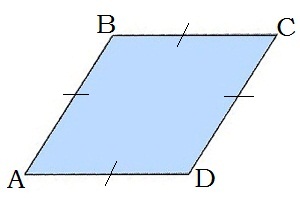
2. Ja paralelograma divas blakusmalas ir vienāda garuma, tad tas ir rombs.
3. Ja paralelograma diagonāles dala uz pusēm katru tā leņķi, tad tas ir rombs (diagonāles ir bisektrises).
4. Ja paralelograma visas malas ir vienāda garuma, tad tas ir rombs.
2. Ja paralelograma divas blakusmalas ir vienāda garuma, tad tas ir rombs.
3. Ja paralelograma diagonāles dala uz pusēm katru tā leņķi, tad tas ir rombs (diagonāles ir bisektrises).
4. Ja paralelograma visas malas ir vienāda garuma, tad tas ir rombs.
Piemērs:
Vai četrstūris, kuram trīs malas ir vienāda garuma ir rombs? Nē.
Piemērs:
Vai paralelograms, kura trīs malas ir vienāda garuma, ir rombs? Jā.
(No trim malām divas noteikti būs blakusmalas, izpildās 2. pazīme)
(No trim malām divas noteikti būs blakusmalas, izpildās 2. pazīme)
