Mediāna — teorija. Matemātika, 8. klase.

Nogriezni, kas savieno trijstūra malas viduspunktu ar pretējo virsotni, sauc par \(mediānu\).

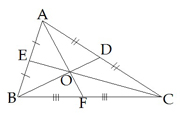
Katram trijstūrim ir trīs mediānas.

Trijstūrī visas mediānas krustojas vienā punktā, kurš sadala katru mediānu attiecībā \(2:1\), skaitot no trijstūra virsotnes:

\frac{BO}{OD} = \frac{AO}{OF} = \frac{CO}{OE} = \frac{2}{1}

Vienkāršāk: "nogrieznis \(CO\) ir divreiz garāks par \(OE\)" vai "\(OE\) ir uz pusi īsāks nekā \(OC\)".

Piemērs:

Aprēķini nogriežņa \(OD\) un \(BD\) garumu, ja \(BO\) ir \(8\) cm (skat. zīm.).

Risinājums:

\frac{BO}{OD} = \frac{2}{1} \frac{8}{OD} = \frac{2}{1} OD = \frac{8}{2} = 4

Var arī risināt ar spriedumiem: \(OD\) ir divas reizes īsāks nekā \(BO\), tātad \(OD = 4\) cm.

Mediāna

BD = BO + OD = 8 + 4 = 12 cm

vai

BD = 3 OD = 12 cm

(jo mediānu veido trīs vienības).

Atradi kļūdu?

4. Mediāna