Divu līdzīgu trijstūru perimetru attiecība ir vienāda ar līdzības koeficientu.
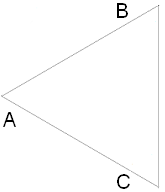
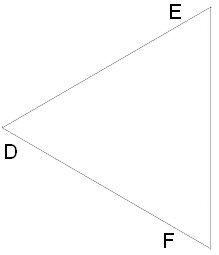
Tas nozīmē, ka līdzīgu trijstūru malu attiecība ir vienāda ar perimetru attiecību.
Ja , tad arī
Divu līdzīgu trijstūru laukumu attiecība ir vienāda ar līdzības koeficienta kvadrātu.
Ja , tad
Piemērs:
Dots: , trijstūri ir regulāri, \(AB = 3\) cm, \(DE = 4\) cm. Noteikt līdzības koeficientu \(k\), perimetru attiecību un trijstūru laukumu attiecību.
Šos rezultātus var iegūt arī, izdarot aprēķinus, bet tas nebūtu racionāli. Pamēģini!
(jo tie ir vienādmalu trijstūri),
tātad arī pēc 1. teorēmas.
, pēc 2. teorēmas.
Šos rezultātus var iegūt arī, izdarot aprēķinus, bet tas nebūtu racionāli. Pamēģini!
- regulāra trijstūra laukuma formula