Talesa teorēma:
"Ja uz vienas leņķa malas atlikti vienādi nogriežņi un caur to galapunktiem novilktas savstarpēji paralēlas taisnes, kas krusto leņķa otru malu, tad tās arī uz leņķa otras malas atšķeļ savstarpēji vienādus nogriežņus."
"Ja uz vienas leņķa malas atlikti vienādi nogriežņi un caur to galapunktiem novilktas savstarpēji paralēlas taisnes, kas krusto leņķa otru malu, tad tās arī uz leņķa otras malas atšķeļ savstarpēji vienādus nogriežņus."
Talesa teorēmu izmanto, lai nogriezni sadalītu vairākās vienādās daļās. Tas ir izdevīgi, ja uz viena nogriežņa ir dotas iedaļas (rūtiņas vai tml.).
Skat. piemērā: uz nogriežņa \(BC\) ir redzamas vienības, bet jāsadala vienādās daļās ir nogrieznis \(AB\).
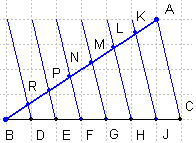
Dots: leņķis \(ABC\).
Sadalīt nogriezni \(AB\) septiņās vienādās daļās.
Vienu leņķa malu (\(BC\)) ērti sadalīt \(7\) vienādās daļās pa rūtiņām:
\(BD = DE = EF = FG = GH = HJ = JC\).
Abus nogriežņu galapunktus savieno, izveidojot \(AC\). Tālāk velk taisnes, kas paralēlas \(AC\), bet sākas punktos-
\(J\), \(H\), \(G\), \(F\), \(E\), \(D\), iegūstot \(7\) paralēlas taisnes.
Sadalīt nogriezni \(AB\) septiņās vienādās daļās.
Vienu leņķa malu (\(BC\)) ērti sadalīt \(7\) vienādās daļās pa rūtiņām:
\(BD = DE = EF = FG = GH = HJ = JC\).
Abus nogriežņu galapunktus savieno, izveidojot \(AC\). Tālāk velk taisnes, kas paralēlas \(AC\), bet sākas punktos-
\(J\), \(H\), \(G\), \(F\), \(E\), \(D\), iegūstot \(7\) paralēlas taisnes.
Ja \(BD = DE = EF = FG = GH = HJ = JC\) un , tad, pēc Talesa teorēmas, \(BR = RP = PN = NM = ML = LK = KA\).