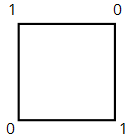
Kvadrāta virsotnēs ierakstīti skaitļi \(0\) un \(1\) tā, kā parādīts zīmējumā. Vienā gājienā jebkuriem skaitļiem, kas atrodas pie divām blakus esošām virsotnēm, drīkst pieskaitīt skaitli 7. Vai ir iespējams, ka, izdarot vairākus šādus gājienus, pie visām kvadrāta virsotnēm iegūs vienādus skaitļus?
Risinām kopā!
Ar \(A\) apzīmēsim skaitļu summu pie tām virsotnēm, pie kurām sākumā uzrakstīti vieninieki,
Ar \(B\) apzīmēsim skaitļu summu pie tām virsotnēm, pie kurām sākumā pierakstītas nulles.
Sākumā \(A =\), \(B =\) un starpība \(A-B =\)
Pēc pirmā gājiena
\(A=\)
\(B=\)
Turpinot mēģinājumus, var ievērot, ka gan summa \(A\), gan summa \(B\) pēc katra gājiena palielinās par skaitli .
Var secināt, ka pēc katra gājiena \(A-B =\).
Tas nozīmē, ka visās četrās virsotnēs būt vienādi skaitļi.
Atsauce:
Lai iesniegtu atbildi un redzētu rezultātus, Tev nepieciešams autorizēties. Lūdzu, ielogojies savā profilā vai reģistrējies portālā!