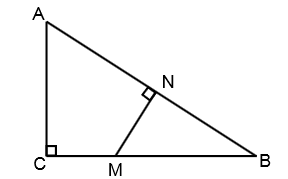
Dots taisnleņķa trijstūris (ar taisno leņķi ). Pret hipotenūzu no tās iekšējā punkta novilkts perpendikuls, kas kateti krusto punktā (sk. att.).
Pierādi, ka
a) ,
b) ,
c) ap četrstūri var apvilkt riņķa līniju un .
Pierādi kopā ar Uzdevumi.lv vai paņem papīra lapu, uzzīmē doto trijstūri un meklē savu risinājumu!
a) Ja leņķi apzīmē ar , tad leņķis un leņķis
Tātad .
b) Pēc līdzības pazīmes, . Uzrakstot līdzīgu trijstūru malu proporciju, iegūst
, seko, ka
c) Ap četrstūri var apvilkt riņķa līniju, jo pretējo summas ir vienādas.
, jo tie ir leņķi, kas balstās uz loka .
Lai iesniegtu atbildi un redzētu rezultātus, Tev nepieciešams autorizēties. Lūdzu, ielogojies savā profilā vai reģistrējies portālā!