Funkciju, kuras vispārīgais veids ir \(y = kx + b\), kur , sauc par lineāru funkciju.
Lineāras funkcijas grafiks ir taisne.
Lineāras funkcijas definīcijas un arī vērtību apgabals ir (visi reālie skaitļi).
Svarīgi!
Ja dota lineāra funkcija \(y = kx + b\), tad \(k\) sauc par taisnes virziena koeficientu, bet \(b\) norāda taisnes krustpunktu ar \(Oy\) asi.
- Ja leņķis, ko veido funkcijas grafiks ar \(Ox\) ass pozitīvo virzienu, ir šaurs, tad \(k > 0\) un funkcija ir augoša (1. zīm.)
- Ja leņķis, ko veido funkcijas grafiks ar \(Ox\) ass pozitīvo virzienu, ir plats, tad \(k < 0\) un funkcija ir dilstoša (2. zīm.)
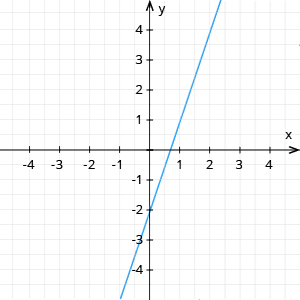
1. zīm.
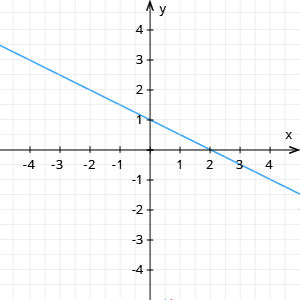
2. zīm.
Ja taišņu virziena koeficienti ir vienādi, tad šīs taisnes ir paralēlas.
Piemērs:
Uzraksti vienādojumu lineārai funkcijai, kura ir paralēla taisnei \(y = 3x\) un krusto \(Oy\) asi punktā \((0;5)\).
Risinājums:
Lineāras funkcijas vispārīgais veids: \(y = kx + b\).
1) Tā kā funkcijas ir dotas paralēlas, tad to virziena koeficienti ir vienādi: \(k = 3\);
2) \(b\) norāda taisnes krustpunktu ar \(Oy\) asi, tā kā \((0;5)\) ir krustpunkts ar \(y\) asi, tad \(b = 5\).
Atbilde: \(y = 3x + 5\)
Ja lineāras funkcijas virziena koeficients \(k = 0\), tad \(y = b\) grafiks ir taisne, kas paralēla \(Ox\) asij.
Piemērs:
Kura no 3. zīmējumā dotajām taisnēm ir funkcija?
Ja \(k = 0\), bet \(b = -2\), iegūst funkciju \(y = -2\).
Koordinātu plaknē var novilkt arī taisni, kas paralēla \(Oy\) asij - \(x = 3\), bet tā nav funkcija (jo vienai argumenta vērtībai atbilst vairāk nekā viena funkcijas vērtība).
3. zīm.
Ja \(b = 0\), tad \(y = kx\), to sauc par tiešo proporcionalitāti.
Tās grafiks ir taisne, kas iet caur koordinātu sākumpunktu.
Piemērs:
Tiešā proporcionalitāte ir ceļa formula ir \(s = vt\). Var teikt, ka ceļš un laiks vai ceļš un ātrums ir tieši proporcionāli lielumi. Vienam lielumam palielinoties (samazinoties), tikpat reizes palielinās (samazinās) arī otrs lielums.
Vēlies skaidrojošus video 9. klases matemātikas tēmām?