Taisnleņķa trijstūrī hipotenūzas garuma kvadrāts vienāds ar abu katešu garumu kvadrātu summu.
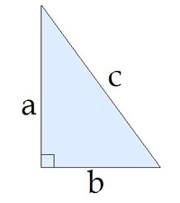
Ja hipotenūza ir \(c\), bet katetes \(a\) un \(b\), tad .
Ja aprēķina kateti, tad .
Atceries:
Ja aprēķina garāko malu — hipotenūzu, tad saskaita.
Ja aprēķina īso malu — kateti, tad atņem.
Taisnleņķa trijstūra pazīme
Ja trijstūra vienas malas garuma kvadrāts vienāds ar abu pārējo malu garumu kvadrātu summu, tad šīs malas pretleņķis ir taisns un trijstūris ir taisnleņķa.
Piemērs:
Aprēķini taisnleņķa trijstūra kateti, ja viena katete ir , bet hipotenūza ir gara.
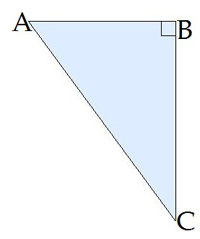
Dots:
,
Jāaprēķina: \(BC\)
Risinājums:
Svarīgi!
Lai risinājumā ietaupītu laiku, atceries biežāk lietotos Pitagora skaitļus!
katete, katete, hipotenūza:
\(3\), \(4\), \(5\)
\(6\), \(8\), \(10\)
\(12\), \(16\), \(20\)
\(5\), \(12\), \(13\)
Piemērs:
Vai trijstūris, kam malu garumi ir \(6\) , \(7\) un \(9\) , ir taisnleņķa?
Izvēlas garāko malu un pārbauda to, vai izpildās Pitagora teorēma:
Neizpildās, tātad šis nav taisnleņķa trijstūris.
Piemērs:
Aprēķini kvadrāta diagonāli, ja dota kvadrāta mala!
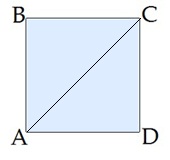
Apzīmē \(BC = CD = DA = AB = a\).
Jāaprēķina: \(AC\)
Trijstūris \(ABC\) ir taisnleņķa trijstūris. Pēc Pitagora teorēmas:
Ja kvadrāta mala ir \(a\), tad šī kvadrāta diagonāle ir .