Augošas un dilstošas skaitļu virknes
Tu ja iepriekš veidoji ritmiskas virknes no dažādiem objektiem. Atkārto to šeit!
Dažādas virknes var veidot arī no skaitļiem.
Skaitļu virkne var būt ar secīgi izvietoties skaitļiem pēc kārtas.
Skaitļu virknē secība var būt:
- augoša – \(1\), \(2\), \(3\), \(4\), \(5\), \(6\), \(7\), \(8\), \(9\), \(10\);
- dilstoša – \(10\), \(9\), \(8\), \(7\), \(6\), \(5\), \(4\), \(3\), \(2\), \(1\).
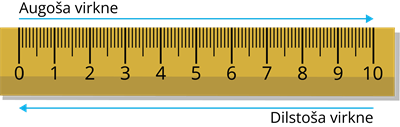
Skaitļu virknes var būt dažādas. Tās var arī veidot, piemēram, uz priekšu un atpakaļ ik pa \(1\), pa \(2\), pa \(5\), vai pa \(10\).
Svarīgi!
Skaitļu virknēs katrs nākamais virknes loceklis pēc kaut kādas likumsakarības saistīts ar iepriekšējo. Būtiski virknes sastāvā ir noteikt likumsakarību un to skaidrot, pamatot.
Ja virknē nākamais skaitlis veidojas, ja pieskaita kādu skaitli, tad veidosies augoša skaitļu virkne.
Piemērs:
Ja virknē nākamais skaitlis veidojas, ja atņem kādu skaitli, tad veidosies dilstoša skaitļu virkne.
\(2\), \(4\), \(6\), \(8\), \(10\), \(12\), \(14\), \(16\), \(18\), \(20\).
Virknes likumsakarība: Katrs nākamais skaitlis veidojas, iepriekšējam pieskaitot klāt \(2\). Tā kā virkne sākas ar \(2\), tad veidojas pāra skaitļu virkne. Augoša skaitļu virkne.
\(1\), \(3\), \(5\), \(7\), \(9\), \(11\), \(13\), \(15\), \(17\), \(19\).
Virknes likumsakarība: Arī šajā virknē katrs nākamais skaitlis veidojas, iepriekšējam pieskaitot klāt \(2\). Bet, tā kā šī virkne sākas ar \(1\), tad veidojas nepāra skaitļu virkne. Augoša skaitļu virkne.
\(5\), \(10\), \(15\), \(20\), \(25\), \(30\), \(35\), \(40\), \(45\), \(50\).
Virknes likumsakarība: Katrs nākamais skaitlis veidojas, iepriekšējam pieskaitot klāt \(5\). Augoša skaitļu virkne.
\(10\), \(20\), \(30\), \(40\), \(50\), \(60\), \(70\), \(80\), \(90\), \(100\).
Virknes likumsakarība: Katrs nākamais skaitlis veidojas, iepriekšējam pieskaitot klāt \(10\). Augoša skaitļu virkne.
\(19\), \(16\), \(13\), \(10\), \(7\), \(4\), \(1\).
Virknes likumsakarība: Katrs nākamais skaitlis veidojas, iepriekšējam atņemot \(3\). Dilstoša skaitļu virkne.
Virknes likumsakarība: Katrs nākamais skaitlis veidojas, iepriekšējam pieskaitot klāt \(2\). Tā kā virkne sākas ar \(2\), tad veidojas pāra skaitļu virkne. Augoša skaitļu virkne.
\(1\), \(3\), \(5\), \(7\), \(9\), \(11\), \(13\), \(15\), \(17\), \(19\).
Virknes likumsakarība: Arī šajā virknē katrs nākamais skaitlis veidojas, iepriekšējam pieskaitot klāt \(2\). Bet, tā kā šī virkne sākas ar \(1\), tad veidojas nepāra skaitļu virkne. Augoša skaitļu virkne.
\(5\), \(10\), \(15\), \(20\), \(25\), \(30\), \(35\), \(40\), \(45\), \(50\).
Virknes likumsakarība: Katrs nākamais skaitlis veidojas, iepriekšējam pieskaitot klāt \(5\). Augoša skaitļu virkne.
\(10\), \(20\), \(30\), \(40\), \(50\), \(60\), \(70\), \(80\), \(90\), \(100\).
Virknes likumsakarība: Katrs nākamais skaitlis veidojas, iepriekšējam pieskaitot klāt \(10\). Augoša skaitļu virkne.
\(19\), \(16\), \(13\), \(10\), \(7\), \(4\), \(1\).
Virknes likumsakarība: Katrs nākamais skaitlis veidojas, iepriekšējam atņemot \(3\). Dilstoša skaitļu virkne.
Var veidot arī sarežģītākas skaitļu virknes, kurā gan pieskaita, gan atņem pēc noteikta algoritma, ievērojot ritmu un likumsakarību.
Piemērs:
\(1\), \(3\), \(2\), \(4\), \(3\), \(5\), \(4\).
Virknes likumsakarība: Vispirms pieskaita \(2\), tad atņem \(1\). Tālāk turpina virkni pēc šī iesāktā algoritma.
\(1\) +2 \(= 3\) -1 \(= 2\) +2 \(= 4\) -1 \(= 3\) +2 \(= 5\) -1 \(= 4\)
Vai vari pēc šī algoritma virkni paturpināt pats?
Virknes likumsakarība: Vispirms pieskaita \(2\), tad atņem \(1\). Tālāk turpina virkni pēc šī iesāktā algoritma.
\(1\) +2 \(= 3\) -1 \(= 2\) +2 \(= 4\) -1 \(= 3\) +2 \(= 5\) -1 \(= 4\)
Vai vari pēc šī algoritma virkni paturpināt pats?
Izdomā savu skaitļu virkni! Pastāsti, kāda ir skaitļu virknes likumsakarība, kā tā veidojas. Palūdz kādam savu skaitļu virkni paturpināt!
Skaitļu virknes uz skaitļu taisnes ar slēptiem skaitļiem
Šajā skaitļu taisnē ir redzama skaitļu virkne no \(11\) līdz \(20\). Daži skaitļi ir paslēpušies aiz burtiem \(A\), \(B\), \(C\).
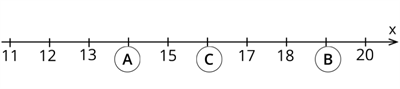
Lai noteiktu, kādi skaitļi ir paslēpušies aiz burtiem, vispirms jānosaka, cik liels ir skaitļu taisnes viens solis. Te nosakām, ka viens solis ir viena vienība jeb katrs nākamais skaitlis veidojies, pie iepriekšējā skaitļa pieskaitot vienu klāt. Tātad aiz burta \(A\) ir paslēpies skaitlis \(14\), jo \(13 + 1 = 14\). Pēc tāda paša principa varam noteikt, ka aiz \(C\) burta ir skaitlis \(16\). Kads tad skaitlis ir paslēpies aiz burta \(C\)?
Ja skaitļu virknē \(1\) solis ir viena vienība, tad vari izmantot arī lineālu, lai atrastu paslēptos skaitļus.

Sarežģītāk ir noteikt paslēptos skaitļus, ja dotajā skaitļu taisnē \(1\) solis ir vairāk nekā viena vienība.
Piemērs:
Šajā skaitļu taisnē redzama skaitļu virkne, kurā parādīti tikai trīs no visiem skaitļiem \(10\), \(20\) un \(50\).

Izpētām vispirms, cik liels ir \(1\) solis. Līdz pirmajam redzamajam skaitlim \(10\) ir divi soļi. Atceries, ka visi soļi skaitļu taisnē ir vienāda lieluma.Tātad šeit \(1\) solis ir \(5 \) vienības liels, jo, ejot divus soļus \(5\) un vēl \(5\), mē nonākam līdz pirmajam zināmajam skaitlim \(10\)/. Zinot, ka viens solis ir\(5\), mēs tālāk varam noteikt arī paslēptos skaitļus, no zināmā pieskaitot vai atņemot \(5\).
\(A\) \(=\) \(20 + 5 + 5 + 5 + 5 = 40\)
\(B\) \(=\) \(50 - 5 = 45\)
Monētu virkne

Papildus vari noskatīties arī tavaklase.lv mācību video par skaitļu virknēm.
