Salīdzināt skaitļus nozīmē pateikt, kurš no tiem ir lielāks. Par diviem atšķirīgiem skaitļiem vienmēr var pateikt, kurš lielāks.
Vienciparu skaitļu salīdzināšana
Visvieglāk skaitļus salīdzināt, skatoties skaitļus uz skaitļu taisnes. Skaitlis uz skaitļu taisnes rāda, cik soļu (vienības nogriežņu) ir no \(0\) līdz konkrētajam skaitlim.

Skaitļu taisne
Katram skaitlim ir noteikta vieta uz skaitļu taisnes, katrs nākamais skaitlis ir lielāks nekā iepriekšējais, jo atrodas tālāk no \(0\). Skaitļu taisnē soļiem jeb vienības garumiem jābūt vienādiem. Šajā skaitļu taisnē viens solis ir vienu vienību liels.
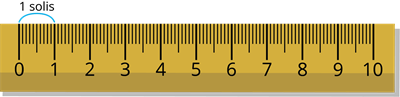
Par skaitļu taisni var izmantot arī lineālu vai mērlenti. Šajā gadījumā skaitļu taisnē viens solis ir \(1\) centimetru liels.
Ja divus skaitļus salīdzina, starp tiem tiek izmantotas atbilstošas salīdzināšanas zīmes:
- mazāks nekā \(<\)
- vienāds ar \(=\)
- lielāks nekā \(>\)
Uz skaitļu tasines izvēlamies skaitli \(4\) un apvelkam to. Pa kreisi no \(4\) skaitļi paliek mazāki, bet pa labi no \(4\) skaitļi paliek lielāki. Tagad salīdzināsim \(4\) ar skaitļiem \(2\) un \(7\).

Vēro, kā uz skaitļu taisnes apvilktie skaitļi tiek salīdzināti!
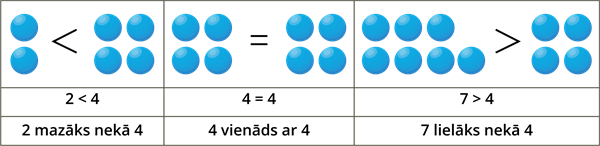
Ja šos konkrētos skaitļus mēs aizvietotu ar burtiem, tad mēs varētu izteikt sakarības arī ar burtiem.
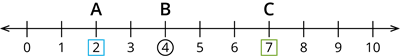
\(A\) ir mazāks nekā \(B\)
\(A\) \(<\) \(B\), jo \(2 < 4\)
\(C\) ir lielāks nekā \(B\)
\(C\) \(>\) \(B\), jo \(7 > 4\)
Skaitļu taisnes var veidot dažādas.
Veidojot skaitļu taisni, būtiski, lai soļi (vienības garumi) būtu vienādi, bet soļa garumu katrā reizē var izvēlēties arī citu. To nosaka atkarībā no tā, cik daudz vai cik lielus skaitļus vēlas parādīt.
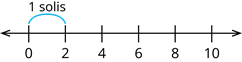
Šajā skaitļu taisnē viens solis ir divu vienību liels.

Šajā skaitļu taisnē viens solis ir desmit vienību liels.
Divciparu skaitļu salīdzināšana
Kā salīdzināt divciparu skaitļus? Piemēram, kā salīdzināt skaitļus \(24\) un \(29\) vai skaitļus \(74\) in \(39\)? Varētu tos atrast uz skaitļu taisnes, piemēram, uz mērlentes un salīdzināt. Bet mērlente ne vienmēr būs pieejama, tāpēc apgūsim citus salīdzināšanas veidus.
Tu jau zini, ka divciparu skaitļi sastāv no desmitiem un vieniem. Ja nepieciešams, atkārto to šeit!
Lai salīdzinātu divciparu skaitļus, jāsalīdzina vienus un desmitus tajos. Šeit svarīgi vispirms noskaidrot, vai abos skaitļos, ko salīdzināsim, desmiti ir vienādi vai atšķirīgi.

\(24\) ir mazāks nekā \(29\), tātad \(29\) ir lielāks nekā \(24\)
\(74\) ir lielāks nekā \(39\), tātad \(39\) ir mazāks nekā \(74\)
Skaitļus var salīdzināt arī, izmantojot simta kvadrātu. Salīdzināsim skaitļus \(57\) un \(75\)! Vispirms atradīsim \(57\). Visi skaitļi, kas ir pa kreisi un uz augšu no \(57\), ir mazāki nekā \(57\). Savukārt skaitļi pa labi un uz leju no \(57\) ir lielāki nekā \(57\).
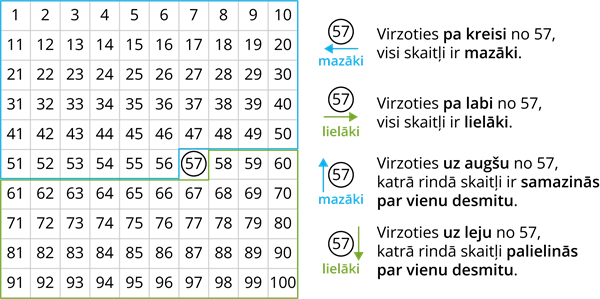
Tātad secinām, ka \(57\) ir mazāks nekā \(75\) jeb \(75\) it lielāks nekā \(57\).
\(57 < 75\)
\(75 > 57\)
Atceries!

"Viņš vienmēr gatavs apēst lielāko."
Katru no attieksmēm var uzrakstīt arī apgrieztā veidā.

Papildus vari noskatīties arī tavaklase.lv mācību video par skaitļu salīdzināšanu.
