Svarīgi!
Atceries! Reizināt var tikai tad, ja ir vienādi saskaitāmie, vienādi daudzumi, kas jāsaskaita.
\(4\) \(+\) \(4\) \(=\) \(8\)
Ar reizināšanu to var pierakstīt divejādi:
| Pa \(4\) āboli ņem \(2\) reizes. | \(2\) reizes ņem pa \(4\) āboli. |
| \(4\) \(·\) \(2\) \(=\) \(8\) | \(2\) \(·\) \(4\) \(=\) \(8\) |
Svarīgi!
Atceries! Dalīt nozīmē sadalīt vienādās daļās un pateikt, cik ir katrā daļā, vai dalīt daļās pa noteiktu daudzumu un pateikt, cik ir daļu.
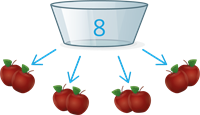
\(8\) ābolus sadalīt pa \(2\) katrā daļā.
\(8\) \(:\) \(2\) \(=\) \(4\) (vienādas daļas)
vai
\(8\) ābolus sadalīt \(4\) vienādās daļās.
\(8\) \(:\) \(4\) \(=\) \(2\) (āboli katrā daļā)
Reizināšana un dalīšana ir savstarpēji saistīta. Uzmanīgi izpēti vēlreiz visus augstāk minētos piemērus ar āboliem! Izpēti likumsakarības!
Draudzīgās vienādības
\(4\) \(·\) \(2\) \(=\) \(8\) \(2\) \(·\) \(4\) \(=\) \(8\) \(8\) \(:\) \(2\) \(=\) \(4\) \(8\) \(:\) \(4\) \(=\) \(2\) |  |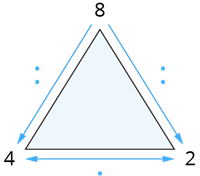
Lai Tu būtu apguvis prasmi reizināt un dalīt tabulas robežās, Tev vēl jāiemācās pēc tāda paša principa reizināt un dalīt ar \(6, 7, 8, 9, 10\).
Daudzus piemērus Tu jau zini. Ja esi kārtīgi apguvis reizināšanu līdz \(5\), tad atliek apgūt tikai tos, kas ir zilā krāsā.
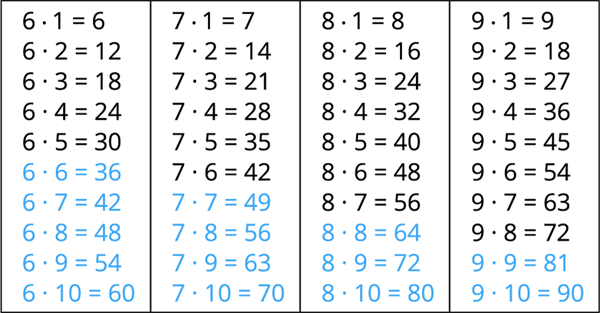
Modelē pats reizināšanas darbību ar rūtiņām, iegūstot rezultātu šeit!
Mācies visu reizināšanas tabulu!
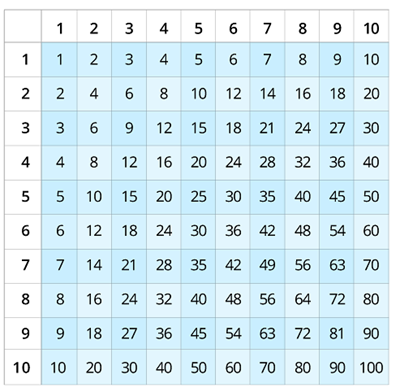
Svarīgi!
Atkārto darbības locekļu nosaukumus!
Vēlies skaidrojošus video 3. klases matemātikas tēmām?