Izpēti likumsakarības, kad skaitlis jāreizina vai jādala ar \(1, 0, 10\)! Tos izprotot, Tev nevajadzēs tos mācīties no galvas.
Reizināšana un dalīšana ar \(1\)
Ja kādu skaitli reizina ar \(1\), tad iegūst to pašu skaitli.
\(a · 1 = a\)
Ja kādu skaitli dala ar \(1\), tad iegūst to pašu skaitli.
\(a : 1 = a\)
Reizināt ar \(1\) nozīmē ņemt kādu skaitli \(1\) reizi. Tas nozīmē, ka rezultātā būs tas pats skaitlis.
Piemērs:
Uz galda bija āboli. Meitene paņēma \(3\) ābolus vienu reizi. Cik ābolu meitenei?
\(3 · 1 = 3\) (āboli)
\(3\) zēniem ir katram pa vienam ābolam. Cik ābolu kopā?
\(3 · 1 = 3\) (āboli)
\(3 · 1 = 3\) (āboli)

Dalīt ar \(1\) nozīmē, ka visu daudzumu mēs, piemēram, sadalām vienā traukā vai iedodam vienam cilvēkam. Rezultātā būs tas pats daudzums.
Piemērs:
Meitenei ir \(2\) āboli un viņa tos abus sadalīja (ielika) vienā grozā. Cik ābolu tagad ir grozā?
\(2 : 1 = 2\) (āboli)
\(2 : 1 = 2\) (āboli)

Reizināšana ar \(0\)
Ja kādu skaitli reizina ar \(0\), rezultāts ir \(0\).
\(a · 0 = 0\)
Dalīt kādu skaitli ar \(0\) nav iespējams!
\(a : 0\) nav iespējams, jo nav tāda skaitļa, kuru reizinot ar 0 iegūtu a.
\(a : 0\) nav iespējams, jo nav tāda skaitļa, kuru reizinot ar 0 iegūtu a.
Reizināt ar \(0\) nozīmē, ka izvēlēto skaitli neņem nevienu reizi. Tātad rezultāts būs nulle (nekā nebūs).
Piemērs:
Grozā ir \(4\) āboli. Meitene ābolus nepaņēma nevienu reizi. Cik tagad meitenei ābolu?
\(4 · 0 = 0\) (āboli)

Viencipara skaitļa reizināšana un dalīšana ar \(10\)
Izpēti uzmanīgi! Kas mainās, ja viencipara skaitli reizina ar \(10\)?
Reizinot viencipara skaitli ar \(10\), iegūstam tikpat daudz desmitus.
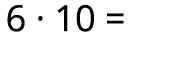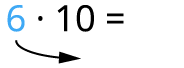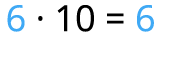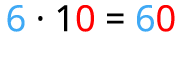
Dalot pilnu desmitu ar \(10\), iegūstam tikpat daudz vienus. Ja proti reizināt ar \(10\), tad tā ir pretēja darbība.