Taisnstūra paralēlskaldņa izmēru nosaka trīs šķautņu, kas iziet no vienas virsotnes, garumi.
Šo šķautņu garumus sauc par platumu, garumu un augstumu. Vienā vārdā tās sauc par dimensijām.
Izmantojot paralēlskaldņa izmērus, var aprēķināt tā tilpumu. Tilpums rāda, cik daudz vielas var iepildīt dotajā traukā.
Taisnstūra paralēlskaldņa tilpumu aprēķina, sareizinot visas trīs dimensijas.
Tilpums ir vienāds ar garuma, platuma un augstuma reizinājumu.
Ja garumu apzīmē ar burtu \(a\), platumu ar burtu \(b\), bet augstumu ar burtu \(c\), tad tilpumu \(V\) aprēķina ar formulu:
Dots taisnstūra paralēlskaldnis , tā dimensijas ir, piemēram, \(DA\), \(DC\) un \(DK\).
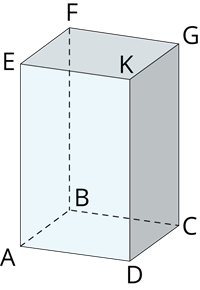
Aprēķini taisnstūra paralēlskaldņa tilpumu, ja
\(AD\) \(=\) \(3\) \(cm\), \(DC\) \(=\) \(4\) \(cm\) un \(DK\) \(=\) \(8\) \(cm\).
Redzam, ka dotas visas trīs dimensijas \(a\) \(=\) \(3\) \(cm\), \(b\) \(=\) \(4\) \(cm\), \(c\) \(=\) \(8\) \(cm\).
Tātad .Ievēro, ka tilpuma mērvienība ir kubikcentimetrs, jo izmēri bija doti centimetros.
Ja taisnstūra paralēlskaldnim visas skaldnes ir kvadrāti, tad šādu ģeometrisko ķermeni sauc par kubu.
Kubam visas trīs dimensijas (platums, garums un augstums) ir vienāda garuma.
Aprēķini tāda kuba tilpumu, kura šķautne ir \(5\) \(cm\).
Tā kā dots kubs, tad platums, garums un augstums ir \(5\) \(cm\).
\(a\) \(=\) \(b\) \(=\) \(c\) \(=\) \(5\) \(cm\).
.
Var arī rakstīt, ka
.